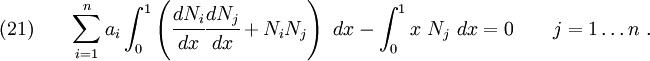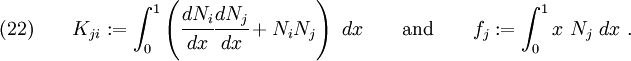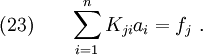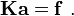Nonlinear finite elements/Bubnov Galerkin method
< Nonlinear finite elements(Bubnov)-Galerkin Method for Problem 2
The Bubnov-Galerkin method is the most widely used weighted average method. This method is the basis of most finite element methods.
The finite-dimensional Galerkin form of the problem statement of our second order ODE is :
Since the basis functions (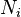 ) are known and linearly independent, the approximate solution
) are known and linearly independent, the approximate solution 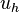 is completely determined once the constants (
is completely determined once the constants (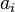 ) are known.
) are known.
The Galerkin method provides a great way of constructing solutions. But the question is: how do we choose 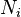 so that these functions are not only linearly independent but arbitrary? Since the solution is expressed as a sum of these functions, the accuracy of our result depends strongly on the choice of
so that these functions are not only linearly independent but arbitrary? Since the solution is expressed as a sum of these functions, the accuracy of our result depends strongly on the choice of 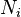 .
.
Let the trial solution take the form,
According to the Bubnov-Galerkin approach, the weighting function also takes a similar form
Plug these values into the weak form to get
or
or
Taking the sums and constants outside the integrals and rearranging, we get
Since the 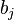 s are arbitrary, the quantity inside the square brackets must be zero. That is
s are arbitrary, the quantity inside the square brackets must be zero. That is
Let us define
Then we get a set of simultaneous linear equations
In matrix form,
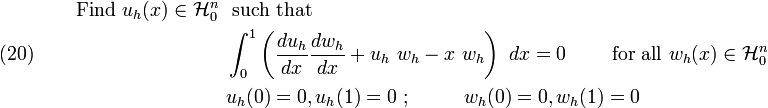
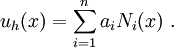
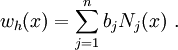
![\int^1_0 \left[\left(\sum_{i=1}^n a_i\cfrac{dN_i}{dx}\right)
\left(\sum_{j=1}^n b_j\cfrac{dN_j}{dx}\right) +
\left(\sum_{i=1}^n a_i N_i\right)
\left(\sum_{j=1}^n b_j N_j \right) -
x \left(\sum_{j=1}^n b_j N_j\right)\right]~dx = 0](../I/m/d85f0965ef03593abbd8bab6c60ff1e9.png)
![\int^1_0 \left[\sum_{j=1}^n b_j
\left(\cfrac{dN_j}{dx} \sum_{i=1}^n a_i\cfrac{dN_i}{dx} +
N_j \sum_{i=1}^n a_i N_i -
x~N_j
\right)
\right] ~dx = 0](../I/m/a2bacabb4daf3111ffb02548c5f21ddb.png)
![\int^1_0 \left[\sum_{j=1}^n b_j
\left(\sum_{i=1}^n \left(a_i\cfrac{dN_j}{dx} \cfrac{dN_i}{dx} +
a_i N_j N_i\right) - x~N_j
\right)
\right] ~dx = 0 ~.](../I/m/856cd2d93d5348ab45cceb565f14269d.png)
![\sum_{j=1}^n b_j \left[\sum_{i=1}^n a_i \int^1_0
\left(\cfrac{dN_i}{dx} \cfrac{dN_j}{dx} +
N_i N_j\right)~dx - \int^1_0 x~N_j~dx \right] = 0 ~.](../I/m/56940b74fe499a5722038a2db36003cd.png)