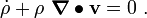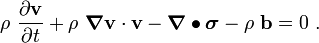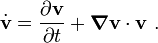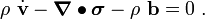Nonlinear finite elements/Balance of linear momentum
< Nonlinear finite elementsStatement of the balance of linear momentum
The balance of linear momentum can be expressed as:
where 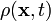 is the mass density,
is the mass density, 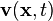 is the velocity,
is the velocity,
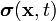 is the Cauchy stress, and
is the Cauchy stress, and 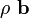 is the body force
density.
is the body force
density.
Proof
Recall the general equation for the balance of a physical quantity
In this case the physical quantity of interest is the momentum density,
i.e., 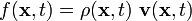 . The source of momentum flux
at the surface is the surface traction, i.e.,
. The source of momentum flux
at the surface is the surface traction, i.e., 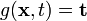 . The
source of momentum inside the body is the body force, i.e.,
. The
source of momentum inside the body is the body force, i.e.,
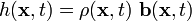 . Therefore, we have
. Therefore, we have
The surface tractions are related to the Cauchy stress by
Therefore,
Let us assume that  is an arbitrary fixed control volume. Then,
is an arbitrary fixed control volume. Then,
Now, from the definition of the tensor product we have (for all vectors
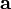 )
)
Therefore,
Using the divergence theorem
we have
or,
Since  is arbitrary, we have
is arbitrary, we have
Using the identity
we get
or,
Using the identity
we get
From the definition
we have
Hence,
or,
The material time derivative of 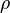 is defined as
is defined as
Therefore,
From the balance of mass, we have
Therefore,
The material time derivative of 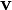 is defined as
is defined as
Hence,
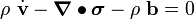
![\cfrac{d}{dt}\left[\int_{\Omega} f(\mathbf{x},t)~\text{dV}\right] =
\int_{\partial{\Omega}} f(\mathbf{x},t)[u_n(\mathbf{x},t) - \mathbf{v}(\mathbf{x},t)\cdot\mathbf{n}(\mathbf{x},t)]~\text{dA} +
\int_{\partial{\Omega}} g(\mathbf{x},t)~\text{dA} + \int_{\Omega} h(\mathbf{x},t)~\text{dV} ~.](../I/m/3c69e1cd86d9e8ff87d1d8359eae78da.png)
![\cfrac{d}{dt}\left[\int_{\Omega} \rho~\mathbf{v}~\text{dV}\right] =
\int_{\partial{\Omega}} \rho~\mathbf{v}[u_n - \mathbf{v}\cdot\mathbf{n}]~\text{dA} +
\int_{\partial{\Omega}} \mathbf{t}~\text{dA} + \int_{\Omega} \rho~\mathbf{b}~\text{dV} ~.](../I/m/0e03ae2f810ca7ed8bf15d33adc74b2e.png)
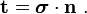
![\cfrac{d}{dt}\left[\int_{\Omega} \rho~\mathbf{v}~\text{dV}\right] =
\int_{\partial{\Omega}} \rho~\mathbf{v}[u_n - \mathbf{v}\cdot\mathbf{n}]~\text{dA} +
\int_{\partial{\Omega}} \boldsymbol{\sigma}\cdot\mathbf{n}~\text{dA} + \int_{\Omega} \rho~\mathbf{b}~\text{dV} ~.](../I/m/2a8d0e822b044395487eafd52c627ebf.png)
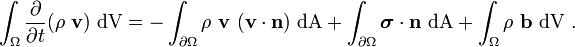
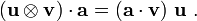
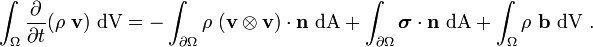
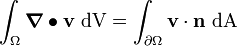
![\int_{\Omega} \frac{\partial }{\partial t}(\rho~\mathbf{v})~\text{dV} =
- \int_{\Omega} \boldsymbol{\nabla} \bullet [\rho~(\mathbf{v}\otimes\mathbf{v})]~\text{dV} +
\int_{\Omega} \boldsymbol{\nabla} \bullet \boldsymbol{\sigma}~\text{dV} + \int_{\Omega} \rho~\mathbf{b}~\text{dV}](../I/m/610ed34ab62cda04214e244e6f01e83a.png)
![\int_{\Omega}\left[
\frac{\partial }{\partial t}(\rho~\mathbf{v}) + \boldsymbol{\nabla} \bullet [(\rho~\mathbf{v})\otimes\mathbf{v})] -
\boldsymbol{\nabla} \bullet \boldsymbol{\sigma} - \rho~\mathbf{b}\right]~\text{dV} = 0 ~.](../I/m/fbbb54174df0e361facc02048500c74f.png)
![\frac{\partial }{\partial t}(\rho~\mathbf{v}) + \boldsymbol{\nabla} \bullet [(\rho~\mathbf{v})\otimes\mathbf{v})] -
\boldsymbol{\nabla} \bullet \boldsymbol{\sigma} - \rho~\mathbf{b} = 0~.](../I/m/e9d36ce2cb41d65b12c2668384567579.png)
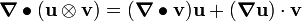
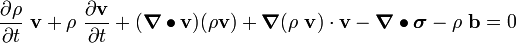
![\left[\frac{\partial \rho}{\partial t} + \rho~\boldsymbol{\nabla} \bullet \mathbf{v}\right]\mathbf{v} +
\rho~\frac{\partial \mathbf{v}}{\partial t} + \boldsymbol{\nabla} (\rho~\mathbf{v})\cdot\mathbf{v} -
\boldsymbol{\nabla} \bullet \boldsymbol{\sigma} - \rho~\mathbf{b} = 0](../I/m/3e1c5ce182a3d22ba13dee31610a133a.png)
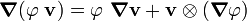
![\left[\frac{\partial \rho}{\partial t} + \rho~\boldsymbol{\nabla} \bullet \mathbf{v}\right]\mathbf{v} +
\rho~\frac{\partial \mathbf{v}}{\partial t} +
\left[\rho~\boldsymbol{\nabla}\mathbf{v} + \mathbf{v}\otimes(\boldsymbol{\nabla} \rho)\right]\cdot\mathbf{v} -
\boldsymbol{\nabla} \bullet \boldsymbol{\sigma} - \rho~\mathbf{b} = 0](../I/m/351eff450dc8ac6ef78fbb01f087fc65.png)
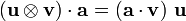
![[\mathbf{v}\otimes(\boldsymbol{\nabla} \rho)]\cdot\mathbf{v} = [\mathbf{v}\cdot(\boldsymbol{\nabla} \rho)]~\mathbf{v} ~.](../I/m/ace826f1c573c89e3e07511d755ae7f5.png)
![\left[\frac{\partial \rho}{\partial t} + \rho~\boldsymbol{\nabla} \bullet \mathbf{v}\right]\mathbf{v} +
\rho~\frac{\partial \mathbf{v}}{\partial t} +
\rho~\boldsymbol{\nabla}\mathbf{v}\cdot\mathbf{v} +[\mathbf{v}\cdot(\boldsymbol{\nabla} \rho)]~\mathbf{v} -
\boldsymbol{\nabla} \bullet \boldsymbol{\sigma} - \rho~\mathbf{b} = 0](../I/m/e5471897155534d1ba0da297541eba2e.png)
![\left[\frac{\partial \rho}{\partial t} + \boldsymbol{\nabla} \rho\cdot\mathbf{v} + \rho~\boldsymbol{\nabla} \bullet \mathbf{v}\right]\mathbf{v} +
\rho~\frac{\partial \mathbf{v}}{\partial t} + \rho~\boldsymbol{\nabla}\mathbf{v}\cdot\mathbf{v} -
\boldsymbol{\nabla} \bullet \boldsymbol{\sigma} - \rho~\mathbf{b} = 0 ~.](../I/m/6f804c907e5cedf57c9396b830c89a65.png)
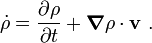
![\left[\dot{\rho} + \rho~\boldsymbol{\nabla} \bullet \mathbf{v}\right]\mathbf{v} +
\rho~\frac{\partial \mathbf{v}}{\partial t} + \rho~\boldsymbol{\nabla}\mathbf{v}\cdot\mathbf{v} -
\boldsymbol{\nabla} \bullet \boldsymbol{\sigma} - \rho~\mathbf{b} = 0 ~.](../I/m/4c0674efbe74bd5d2f0bc3fa6530d062.png)