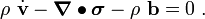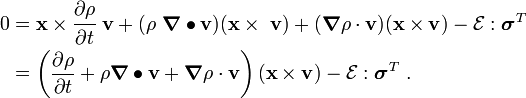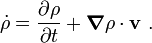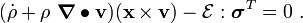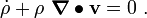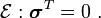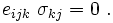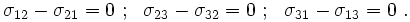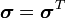Nonlinear finite elements/Balance of angular momentum
< Nonlinear finite elementsStatement of the balance of angular momentum
The balance of angular momentum in an inertial frame can be expressed as:
Proof
We assume that there are no surface couples on  or body couples
in
or body couples
in  . Recall the general balance equation
. Recall the general balance equation
In this case, the physical quantity to be conserved the angular momentum
density, i.e., 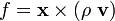 .
The angular momentum source at the surface is then
.
The angular momentum source at the surface is then
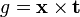 and the angular momentum source inside the body
is
and the angular momentum source inside the body
is  . The angular momentum and moments are
calculated with respect to a fixed origin. Hence we have
. The angular momentum and moments are
calculated with respect to a fixed origin. Hence we have
Assuming that  is a control volume, we have
is a control volume, we have
Using the definition of a tensor product we can write
Also,  . Therefore we have
. Therefore we have
Using the divergence theorem, we get
To convert the surface integral in the above equation into a volume integral, it is convenient to use index notation. Thus,
where ![[~]_i](../I/m/66ca833eed53c7bfd96b2a2d3e74eccd.png) represents the
represents the  -th component of the vector. Using
the divergence theorem
-th component of the vector. Using
the divergence theorem
Differentiating,
Expressed in direct tensor notation,
where  is the third-order permutation tensor.
Therefore,
is the third-order permutation tensor.
Therefore,
or,
The balance of angular momentum can then be written as
Since  is an arbitrary volume, we have
is an arbitrary volume, we have
or,
Using the identity,
we get
The second term on the right can be further simplified using index notation as follows.
Therefore we can write
The balance of angular momentum then takes the form
or,
or,
The material time derivative of 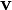 is defined as
is defined as
Therefore,
Also, from the conservation of linear momentum
Hence,
The material time derivative of 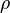 is defined as
is defined as
Hence,
From the balance of mass
Therefore,
In index notation,
Expanding out, we get
Hence,
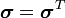
![\cfrac{d}{dt}\left[\int_{\Omega} f(\mathbf{x},t)~\text{dV}\right] =
\int_{\partial{\Omega}} f(\mathbf{x},t)[u_n(\mathbf{x},t) - \mathbf{v}(\mathbf{x},t)\cdot\mathbf{n}(\mathbf{x},t)]~\text{dA} +
\int_{\partial{\Omega}} g(\mathbf{x},t)~\text{dA} + \int_{\Omega} h(\mathbf{x},t)~\text{dV} ~.](../I/m/3c69e1cd86d9e8ff87d1d8359eae78da.png)
![\cfrac{d}{dt}\left[\int_{\Omega} \mathbf{x}\times(\rho~\mathbf{v})~\text{dV}\right] =
\int_{\partial{\Omega}} [\mathbf{x}\times(\rho~\mathbf{v})]
[u_n - \mathbf{v}\cdot\mathbf{n}]~\text{dA} +
\int_{\partial{\Omega}} \mathbf{x}\times\mathbf{t}~\text{dA} +
\int_{\Omega} \mathbf{x}\times(\rho~\mathbf{b})~\text{dV} ~.](../I/m/440422d8cd4c851a9435d8fb461e363a.png)
![\int_{\Omega} \mathbf{x}\times\left[\cfrac{\partial}{\partial t}(\rho~\mathbf{v})\right]~\text{dV} =
- \int_{\partial{\Omega}} [\mathbf{x}\times(\rho~\mathbf{v})][\mathbf{v}\cdot\mathbf{n}]~\text{dA} +
\int_{\partial{\Omega}} \mathbf{x}\times\mathbf{t}~\text{dA} +
\int_{\Omega} \mathbf{x}\times(\rho~\mathbf{b})~\text{dV} ~.](../I/m/38aeddc7dcb7d77ce46e166682c0d4a8.png)
![[\mathbf{x}\times(\rho~\mathbf{v})][\mathbf{v}\cdot\mathbf{n}] =
[[\mathbf{x}\times(\rho~\mathbf{v})]\otimes\mathbf{v}]\cdot\mathbf{n} ~.](../I/m/b62f8cb0f3e29c3a1073ad5a29dd5bea.png)
![\int_{\Omega} \mathbf{x}\times\left[\cfrac{\partial}{\partial t}(\rho~\mathbf{v})\right]~\text{dV} =
- \int_{\partial{\Omega}} [[\mathbf{x}\times(\rho~\mathbf{v})]\otimes\mathbf{v}]\cdot\mathbf{n} ~\text{dA}
+ \int_{\partial{\Omega}} \mathbf{x}\times(\boldsymbol{\sigma}\cdot\mathbf{n})~\text{dA}
+ \int_{\Omega} \mathbf{x}\times(\rho~\mathbf{b})~\text{dV} ~.](../I/m/ecde718f75df1e68603e102e6d2ca6e6.png)
![\int_{\Omega} \mathbf{x}\times\left[\cfrac{\partial}{\partial t}(\rho~\mathbf{v})\right]~\text{dV} =
- \int_{\Omega} \boldsymbol{\nabla} \bullet [[\mathbf{x}\times(\rho~\mathbf{v})]\otimes\mathbf{v}]~\text{dV}
+ \int_{\partial{\Omega}} \mathbf{x}\times(\boldsymbol{\sigma}\cdot\mathbf{n})~\text{dA}
+ \int_{\Omega} \mathbf{x}\times(\rho~\mathbf{b})~\text{dV} ~.](../I/m/a31af91be521b0c85df73f1015558a45.png)
![\left[\int_{\partial{\Omega}} \mathbf{x}\times(\boldsymbol{\sigma}\cdot\mathbf{n})~\text{dA}\right]_i =
\int_{\partial{\Omega}} e_{ijk}~x_j~\sigma_{kl}~n_l~\text{dA}=
\int_{\partial{\Omega}} A_{il}~n_l~\text{dA}=
\int_{\partial{\Omega}} \boldsymbol{A}\cdot\mathbf{n}~\text{dA}](../I/m/5616ce5ea89500e4e680afb2bc05caa6.png)
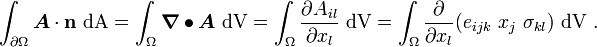
![\int_{\partial{\Omega}} \boldsymbol{A}\cdot\mathbf{n}~\text{dA}
= \int_{\Omega} \left[
e_{ijk}~\delta_{jl}~\sigma_{kl} +
e_{ijk}~x_j~\frac{\partial \sigma_{kl}}{\partial x_l}\right]~\text{dV}
= \int_{\Omega} \left[
e_{ijk}~\sigma_{kj} +
e_{ijk}~x_j~\frac{\partial \sigma_{kl}}{\partial x_l}\right]~\text{dV}
= \int_{\Omega} \left[
e_{ijk}~\sigma_{kj} +
e_{ijk}~x_j~[\boldsymbol{\nabla} \bullet \boldsymbol{\sigma}]_l\right]~\text{dV} ~.](../I/m/c83336db34b6a6f95786d0c71a313d2b.png)
![\int_{\partial{\Omega}} \boldsymbol{A}\cdot\mathbf{n}~\text{dA}
= \int_{\Omega} \left[
[\mathcal{E}:\boldsymbol{\sigma}^T]_i + [\mathbf{x}\times(\boldsymbol{\nabla} \bullet \boldsymbol{\sigma})]_i\right]~\text{dV}](../I/m/3e0059d70978acedc7b6a1e73304a10d.png)
![\left[\int_{\partial{\Omega}} \mathbf{x}\times(\boldsymbol{\sigma}\cdot\mathbf{n})~\text{dA}\right]_i =
= \int_{\Omega} \left[
[\mathcal{E}:\boldsymbol{\sigma}^T]_i + [\mathbf{x}\times(\boldsymbol{\nabla} \bullet \boldsymbol{\sigma})]_i\right]~\text{dV}](../I/m/bef4a82ac9f98da5b7707d410d303af4.png)
![\int_{\partial{\Omega}} \mathbf{x}\times(\boldsymbol{\sigma}\cdot\mathbf{n})~\text{dA} =
= \int_{\Omega} \left[
\mathcal{E}:\boldsymbol{\sigma}^T + \mathbf{x}\times(\boldsymbol{\nabla} \bullet \boldsymbol{\sigma})\right]~\text{dV} ~.](../I/m/dfac2623f1f88e8edb0239ec6f231bd0.png)
![\int_{\Omega} \mathbf{x}\times\left[\cfrac{\partial}{\partial t}(\rho~\mathbf{v})\right]~\text{dV} =
- \int_{\Omega} \boldsymbol{\nabla} \bullet [[\mathbf{x}\times(\rho~\mathbf{v})]\otimes\mathbf{v}]~\text{dV}
+ \int_{\Omega} \left[
\mathcal{E}:\boldsymbol{\sigma}^T + \mathbf{x}\times(\boldsymbol{\nabla} \bullet \boldsymbol{\sigma})\right]~\text{dV}
+ \int_{\Omega} \mathbf{x}\times(\rho~\mathbf{b})~\text{dV} ~.](../I/m/a6eebb451760e65b691b97a5b29961de.png)
![\mathbf{x}\times\left[\cfrac{\partial}{\partial t}(\rho~\mathbf{v})\right] =
- \boldsymbol{\nabla} \bullet [[\mathbf{x}\times(\rho~\mathbf{v})]\otimes\mathbf{v}]
+ \mathcal{E}:\boldsymbol{\sigma}^T + \mathbf{x}\times(\boldsymbol{\nabla} \bullet \boldsymbol{\sigma})
+ \mathbf{x}\times(\rho~\mathbf{b})](../I/m/d3e2623c5d6f348e49b45632c56f7ccb.png)
![{\mathbf{x}}\times
{\left[\frac{\partial }{\partial t}(\rho~\mathbf{v}) - \boldsymbol{\nabla} \bullet \boldsymbol{\sigma} - \rho~\mathbf{b} \right]} =
- \boldsymbol{\nabla} \bullet [[\mathbf{x}\times(\rho~\mathbf{v})]\otimes\mathbf{v}]
+ \mathcal{E}:\boldsymbol{\sigma}^T ~.](../I/m/94ad05821984fa1a0805240f5ec2310e.png)
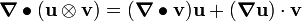
![\boldsymbol{\nabla} \bullet [[\mathbf{x}\times(\rho~\mathbf{v})]\otimes\mathbf{v}] =
(\boldsymbol{\nabla} \bullet \mathbf{v})[\mathbf{x}\times(\rho~\mathbf{v})] +
(\boldsymbol{\nabla} [\mathbf{x}\times(\rho~\mathbf{v})])\cdot\mathbf{v} ~.](../I/m/5cb7db172fb9009b34e9d5dc8a1be107.png)
![\begin{align}
\left[(\boldsymbol{\nabla} [\mathbf{x}\times(\rho~\mathbf{v})])\cdot\mathbf{v}\right]_i =
\left[(\boldsymbol{\nabla} [\rho~(\mathbf{x}\times\mathbf{v})])\cdot\mathbf{v}\right]_i & =
\frac{\partial }{\partial x_l}(\rho~e_{ijk}~x_j~v_k)~v_l \\
& = e_{ijk}\left[
\frac{\partial \rho}{\partial x_l}~x_j~v_k~v_l+
\rho~\frac{\partial x_j}{\partial x_l}~v_k~v_l +
\rho~x_j~\frac{\partial v_k}{\partial x_l}~v_l\right] \\
& = (e_{ijk}~x_j~v_k)~\left(\frac{\partial \rho}{\partial x_l}~v_l\right)+
\rho~(e_{ijk}~\delta_{jl}~v_k~v_l) +
e_{ijk}~x_j~\left(\rho~\frac{\partial v_k}{\partial x_l}~v_l\right) \\
& = [(\mathbf{x}\times\mathbf{v})(\boldsymbol{\nabla} \rho\cdot\mathbf{v}) +
\rho~\mathbf{v}\times\mathbf{v} +
\mathbf{x}\times(\rho~\boldsymbol{\nabla}\mathbf{v}\cdot\mathbf{v})]_i \\
& = [(\mathbf{x}\times\mathbf{v})(\boldsymbol{\nabla} \rho\cdot\mathbf{v}) +
\mathbf{x}\times(\rho~\boldsymbol{\nabla}\mathbf{v}\cdot\mathbf{v})]_i ~.
\end{align}](../I/m/bc8c942f10ae81ef47cb7b728f17362f.png)
![\boldsymbol{\nabla} \bullet [[\mathbf{x}\times(\rho~\mathbf{v})]\otimes\mathbf{v}] =
(\rho~\boldsymbol{\nabla} \bullet \mathbf{v})(\mathbf{x}\times~\mathbf{v}) +
(\boldsymbol{\nabla} \rho\cdot\mathbf{v})(\mathbf{x}\times\mathbf{v}) +
\mathbf{x}\times(\rho~\boldsymbol{\nabla}\mathbf{v}\cdot\mathbf{v})] ~.](../I/m/4407094af4e55c0f3882f95a51d88c56.png)
![{\mathbf{x}}\times
{\left[\frac{\partial }{\partial t}(\rho~\mathbf{v}) - \boldsymbol{\nabla} \bullet \boldsymbol{\sigma} - \rho~\mathbf{b} \right]} =
- (\rho~\boldsymbol{\nabla} \bullet \mathbf{v})(\mathbf{x}\times~\mathbf{v}) -
(\boldsymbol{\nabla} \rho\cdot\mathbf{v})(\mathbf{x}\times\mathbf{v}) -
\mathbf{x}\times(\rho~\boldsymbol{\nabla}\mathbf{v}\cdot\mathbf{v})
+ \mathcal{E}:\boldsymbol{\sigma}^T](../I/m/2456d76f741154e644de2ca7b6cfb571.png)
![{\mathbf{x}}\times
{\left[\frac{\partial }{\partial t}(\rho~\mathbf{v}) + \rho~\boldsymbol{\nabla}\mathbf{v}\cdot\mathbf{v}
- \boldsymbol{\nabla} \bullet \boldsymbol{\sigma} - \rho~\mathbf{b} \right]} =
- (\rho~\boldsymbol{\nabla} \bullet \mathbf{v})(\mathbf{x}\times~\mathbf{v}) -
(\boldsymbol{\nabla} \rho\cdot\mathbf{v})(\mathbf{x}\times\mathbf{v})
+ \mathcal{E}:\boldsymbol{\sigma}^T](../I/m/7c15c30c4d0972d2fd075016beab19f2.png)
![{\mathbf{x}}\times
{\left[\rho\frac{\partial \mathbf{v}}{\partial t} + \frac{\partial \rho}{\partial t}~\mathbf{v} +
\rho~\boldsymbol{\nabla}\mathbf{v}\cdot\mathbf{v}
- \boldsymbol{\nabla} \bullet \boldsymbol{\sigma} - \rho~\mathbf{b} \right]} =
- (\rho~\boldsymbol{\nabla} \bullet \mathbf{v})(\mathbf{x}\times~\mathbf{v}) -
(\boldsymbol{\nabla} \rho\cdot\mathbf{v})(\mathbf{x}\times\mathbf{v})
+ \mathcal{E}:\boldsymbol{\sigma}^T](../I/m/78c441872db6cdd6190422df60bc337b.png)
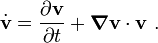
![{\mathbf{x}}\times
{\left[\rho~\dot{\mathbf{v}} - \boldsymbol{\nabla} \bullet \boldsymbol{\sigma} - \rho~\mathbf{b} \right]} =
- \mathbf{x}\times\cfrac{\partial \rho}{\partial t}~\mathbf{v} +
- (\rho~\boldsymbol{\nabla} \bullet \mathbf{v})(\mathbf{x}\times~\mathbf{v}) -
(\boldsymbol{\nabla} \rho\cdot\mathbf{v})(\mathbf{x}\times\mathbf{v})
+ \mathcal{E}:\boldsymbol{\sigma}^T ~.](../I/m/5081063e7c9558421fb4dd5a9cb1e6d4.png)