Nonlinear finite elements

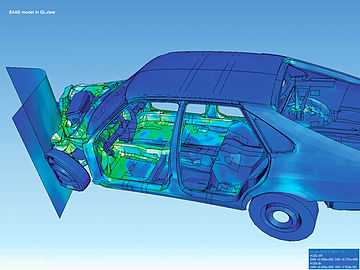
Visualization of how a car deforms in an asymmetrical crash using finite element analysis.

Welcome to this learning project about nonlinear finite elements!

Introduction

Finite element analysis (FEA) is a computer simulation technique used in engineering analysis. It uses a numerical technique called the finite element method (FEM). There are many finite element software packages, both free and proprietary. Development of the finite element method in structural mechanics is usually based on an energy principle such as the virtual work principle or the minimum total potential energy principle. *

Project metadata

Quality resource: this resource is a featured learning resource.

Completion status: this resource has reached a high level of completion.

Educational level: this is a tertiary (university) resource.

Subject classification: this is an engineering resource .

• Suggested Prerequisites:
  • Linear algebra
  • Partial differential equations
  • Introduction to finite elements
  • Continuum mechanics
• Time investment: 6 months
• Portal:Engineering and Technology
• School:Engineering
• Department:Mechanical engineering
• Level: First year graduate

Content summary

This is an introductory course on nonlinear finite element analysis of solid mechanics and heat transfer problems. Nonlinearities can be caused by changes in geometry or be due to nonlinear material behavior. Both types of nonlinearities are covered in this course.

Goals

This learning project aims to.

• provide the mathematical foundations of the finite element formulation for engineering applications (solids, heat, fluids).
• expose students to some of the recent trends and research areas in finite elements.

Here's a short quiz to help you find out what you need to brush up on before you dig into the course:

• Assessment Quiz

Contents

Syllabus and Learning Materials Syllabus and Learning Materials Mathematical Preliminaries Set notation Functions Vectors Matrices Tensors Partial differential equations Variational calculus Linear finite element basics An example: Axially loaded bar Strong form: governing differential equation Weak form: integral equation Approximate solution: Galerkin method Approximate solution: Finite element method More examples: Some model problems Weak form: Weighted residual methods Choosing a weight function Bubnov Galerkin methods Finite element basis functions Example of a finite element approximation A time-dependent problem: the heat equation Steady state heat conduction Weak form of the steady state heat equation Weak form of the time-dependent heat equation Finite element approximation of Poisson equation Finite element approximation of the heat equation Time integration of the heat equation. Nonlinear finite element basics Nonlinearities in solid mechanics An example: Nonlinear deformation of an axially loaded bar Weak form for the nonlinear bar The Newton-Raphson method The Newton method applied to finite elements The Newton method applied to the axially loaded bar Lagrangian and Eulerian descriptions of motion Lagrangian finite elements Motion from the Lagrangian point of view Total Lagrangian approach Updated Lagrangian approach An example: Effect of mesh distortion Solution procedure Special case: Natural vibrations Nonlinear deformation of beams Euler-Bernoulli beams Timoshenko beams Buckling of beams Nonlinear deformation of plates and shells Basic linear plate and shell elements Nonlinear plates and shells Time-dependent deformation of shells Basic continuum mechanics Kinematics Motion, displacement, velocity, acceleration Stresses and strains in one and two dimensions Strains and deformations in three-dimensions Polar decomposition Spectral decompositions of kinematic quantities Volume change and area change Time derivatives and rate quantities Objectivity of kinematic quantities Stress measures and stress rates Stress measures Deviatoric and volumetric stress Objective stress rates Balance laws Overview of balance laws Balance of mass Balance of linear momentum Balance of angular momentum Balance of energy Entropy inequality Constitutive models Objectivity of hyperelastic relations Rate form of hyperelastic relations Nonlinear elasticity Plasticity Viscoplasticity Viscoelasticity. Finite element formulation in three dimensions. Updated Lagrangian formulation Verification and Validation.

Assignments, tests and quizzes Assignments Homework 1 Problem set Solutions Homework 2 Problem set Solutions Homework 3 Problem set Solutions Homework 4 Problem set Hints Solutions Homework 5 Problem set Solutions Homework 6 Problem set Hints Solutions Homework 7 Problem set Hints Solutions Homework 8 Problem set Solutions Homework 9 Problem set Solutions Homework 10 Problem set Solutions Homework 11 Problem set Solutions Tests and Quizzes Quiz 1 Solutions

Textbooks and References

Search for Nonlinear finite elements on Wikipedia.

Search Wikiquote for quotations related to: Nonlinear finite elements

Wikibooks has more on the topic of Nonlinear finite elements.

Look up Nonlinear finite elements in Wiktionary, the free dictionary.

Search Wikinews for news items related to Nonlinear finite elements.

Textbooks

• An Introduction to Nonlinear Finite Element Analysis by J. N. Reddy, Oxford University Press, 2004, ISBN 019852529X.
• Nonlinear Finite Elements for Continua and Structures by T. Belytschko, W. K. Liu, and B. Moran, John Wiley and Sons, 2000.
• Computational Inelasticity by J. C. Simo and T. J. R. Hughes, Springer, 1998.
• The Finite Element Method: Linear Static and Dynamic Finite Element Analysis by T. J. R. Hughes, Dover Publications, 2000.

References

• Finite Element Analysis:
  • K-J. Bathe (1996), Finite Element Procedures, Prentice-Hall. Useful repository of information on nonlinear finite elements.
  • J. N. Reddy (1993), An Introduction to the Finite Element Method, McGraw-Hill. This book is referred to a number of times in one of the texts.
  • O. C. Zienkiewicz and R. L. Taylor (2000), The Finite Element Method: Volume 2 Solid Mechanics, Butterworth-Heinemann. Another excellent repository of information of nonlinear finite elements geared toward the Civil Engineers.
  • J. Bonet and R. Wood (2008), Nonlinear Continuum Mechanics for Finite Element Analysis, Cambridge University Press. This is a particularly good reference for the general continuum mechanics and kinematics involved, with a detailed discussion on material nonlinearities.
  • S. C. Brenner and L. R. Scott (2007), The mathematical theory of finite element methods, vol. 15 of Texts in Applied Mathematics, Springer-Verlag, Classical book on the mathematics foundation of finite element methods.
• Continuum Mechanics:
  • R. M. Brannon (2004), Large Deformation Kinematics. An excellent introduction to kinematics.
  • R. M. Brannon (2004), Rotation. Almost everything you ever wanted to know about rotations.
  • A.J.M Spencer (2004), Continuum Mechanics, Dover Publications. An excellent introduction to continuum mechanics. You should own a copy for your personal library.
  • L.E. Malvern (1969), Introduction to the Mechanics of a Continuous Medium, Prentice-Hall. A good reference for continuum mechanics.
• Mathematics:
  • R. M. Brannon (2004), Elementary Vector and Tensor Analysis for Engineers. This free online book is the best introduction I have seen for vector and tensor analysis for nonlinear mechanics.
  • R. M. Brannon (2004), Curvilinear Coordinates. Very useful if you wish to follow the literature on the nonlinear deformation of shells.
  • B. Daya Reddy (1998), Introductory Functional Analysis: With applications to boundary value problems and finite elements. , Springer-Verlag. Excellent book for engineers who want to understand the terminology used in the finite element literature and how error analysis is done.
  • A.P.S. Selvadurai (2000), Partial Differential Equations in Mechanics 1,2. Springer. Excellent introductory text on partial differential equations with engineers in mind.

Reading List

• Taylor, R.L., Simo, J.C., Zienkiewicz, O.C., and Chan, A.C.H, 1986, The patch test - a condition for assessing FEM convergence, International Journal for Numerical Methods in Engineering, 22, pp. 39-62.
• Simo, J.C. and Vu-Quoc, L., 1986, A three-dimensional finite strain rod model. Part II: Computational Aspects, Computer Methods in Applied Mechanics and Engineering, 58, pp. 79-116.
• Ibrahimbegovic, A., 1995, On finite element implementation of geometrically nonlinear Reissner's beam theory: Three-dimensional curved beam elements, Computer Methods in Applied Mechanics and Engineering, 122, pp. 11-26.
• Buchter, N., Ramm, E., and Roehl, D., 1994, Three-dimensional extension of non-linear shell formulation based on the enhanced assumed strain concept, Int. J. Numer. Meth. Engng., 37, pp. 2551-2568.
• Rouainia, M. and Peric, D., 1998, A computational model for elasto-viscoplastic solids at finite strain with reference to thin shell applications, Int. J. Numer. Meth. Engng., 42, pp. 289-311.

External links

• Gmsh - GPL'd finite element analyzer
• RecurDyn Full Flexible - RecurDyn’s true Finite Element Method combinded with it´s Multi Body Dynamics - FEMBD mechanical system simulation returns more precise dynamic motion results including stress analysis in one single simulation step. It also features flexible body contacts and non-linear deformations.

Hits this month for the page Nonlinear finite elements - (Hold down CTRL key to display in separate tab in browser)