Multivariable Calculus

Please help develop and classify this resource

Learn how you can develop this resource by 209.173.1.25 to teach participants about Multivariable Calculus. Choose a subject, education level, and resource type to classify the resource by. You may learn more about the topic to help you develop and classify the resource from:

Introduction

Multivariable calculus is the study of problems and solutions of continuous functions of more than a single variable. It extends to Vector Analysis and has applications in a wide variety of fields, most notably physics, but also extends to include statistics and finance, biology, and a many other subjects.

Partial Derivatives

If f is a function of more than a single variable we can allow one variable to vary and hold the rest stationary. Differentiating with respect to the one free variable we obtain a partial derivative.

Examples

Given a function
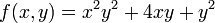
$\,\! f(x,y) = x^2 y^2 +4xy +y^2$
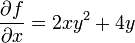
$\frac{\partial f}{\partial x} = 2xy^2 + 4y$
This is the partial derivative of f with respect to x. In each term we hold any variable other than x constant, and differentiate with respect with x.
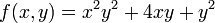
$\,\! f(x,y) = x^2y^2 + 4xy + y^2$
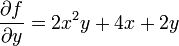
$\frac{\partial f}{\partial y} = 2x^2y + 4x + 2y$

Geometry of Partial Derivatives

if f(x,y) is a surface in 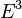$E^3$ , then 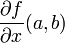$\frac {\partial f}{\partial x}(a,b)$ is the slope of the tangent line (or rate of change_ of the curve traced by the intersection of the plane y=b, and the surface f, in the direction parallel to the x-axis, at the point (a,b).

the function 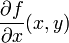$\frac{\partial f}{\partial x}(x,y)$ represents the rate of change of the family of curves traced by the intersection of the planes generated over the domain of y, and the surface f, at the point x.

Symmetry

It is important to notice and provided with out proof, that second derivatives of a function are symmetric, given the function is continuous on the disk that contains the region the function is differentiated over. For a function of 2 variable this means:
$f_{ij} = f_{ji}$

From this further symmetry relations of higher order functions and their derivatives can be derived. For example, f is a function of 3 variables:

f_ijk = f_ikj = f_jik = f_jki

Extrema of Functions

Given a point (a,b) that satisfies
f_x(a,b) = 0 = f_y(a,b)
(a,b) is called a critical point of f.
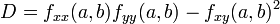
$\,\! D = f_{xx}(a,b)f_{yy}(a,b) - f_{xy}(a,b)^2$
if D > 0 and 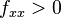$f_{xx} > 0$ , f(a,b) is a local minimum.
if D > 0 and 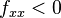$f_{xx} < 0$ , f(a,b) is a local maximum.
otherwise (a,b) is not an extreme, or if D = 0, the test is indeterminate.

This article is issued from Wikiversity - version of the Sunday, October 21, 2012. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.