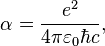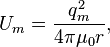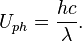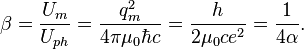Physics/Essays/Fedosin/Monopoles

< Physics < Essays < Fedosin

Monopoles – physical objects that contain the source (charge) of some field isotropically distributed around the respective object. A typical example is an electric monopole with electric charge, the electric field of which is directed radially around and decreases with distance from the monopole inversely proportional to the square of the distance. Similarly, the gravitational monopole has around a radial gravitational field strength and the monopole mass plays the role of gravitational charge. Magnetic monopole is now regarded as a hypothetical object with a non-zero magnetic charge and magnetic field. The torsion monopole has the same status and would be a hypothetical source of torsion charge and gravitational torsion field in the covariant theory of gravitation (or the hypothetical source of gravitomagnetic field in the general relativity). In reality instead of magnetic monopoles the monopole quasiparticles were found in condensed-matter systems [1] and in superfluids. [2] The monopole quasiparticle typically is a magnet with two different magnetic poles at the ends , the north pole and the south pole, which connected by magnetic string. The magnetic fields of poles of the quasiparticle looks like the field of a magnetic monopole.

The hypothetical particle that has both electric and magnetic charge is known as a dion. The object with separated positive and negative charges is the electric dipole, which may be modelled with the help of two electric monopoles. The monopoles represent the first terms in the multipole expansions of different field functions.

Particle level

Charges and masses

Some monopoles can be described with the following fundamental physical charges and masses:

The elementary charge as an electric charge quantum, first proposed by G. Stoney (1881): [3]

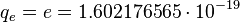q_e = e = 1.602176565\cdot 10^{-19} C.

The fictitious magnetic charge quantum, first proposed by Paul Dirac (1931), [4] which equals to elementary magnetic flux 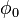\phi_0 and twice magnetic flux quantum \Phi_0 :

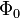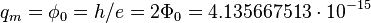q_m = \phi_0 = h/e = 2\Phi_0 = 4.135667513\cdot 10^{-15} J/A,

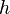where h is the Planck constant.

The proton mass as a gravitational mass quantum: [5]

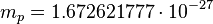m_p = 1.672621777 \cdot 10^{-27} kg.

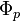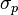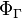The fictitious gravitational torsion quantum, which equals to elementary torsion flux \Phi_p and twice velocity circulation quantum \sigma_p and strong gravitational torsion flux quantum \Phi_\Gamma  :

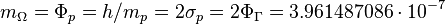m_{\Omega} = \Phi_p = h/m_p = 2\sigma_p =2 \Phi_\Gamma = 3.961487086\cdot 10^{-7} m2/s.

The electron mass as a gravitational mass quantum:

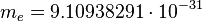m_e = 9.10938291\cdot 10^{-31} kg.

The fictitious gravitational torsion quantum related to electron:

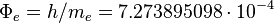\Phi_e = h/m_e = 7.273895098\cdot 10^{-4} m2/s.

Coupling constants

The fine structure constant for electromagnetic interaction of two electric monopoles with elementary charges is:

\alpha = \frac{e^2}{4 \pi \varepsilon_0 \hbar c},

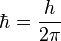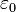where ~ \hbar = \frac {h}{2\pi } is the reduced Planck constant, ~ c is the speed of light in vacuum, ~ \varepsilon_0 is the vacuum permittivity.

The coupling constant for interaction of two nucleons as gravitational monopoles in the field of strong gravitation according to the gravitational model of strong interaction is:

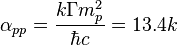\alpha_{pp}= \frac{ k \Gamma m^2_p }{\hbar c }=13.4 k ,

where 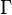~ \Gamma is the strong gravitational constant, 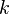~ k is equal to 0.26 for the interaction of two nucleons, and tending to 1 for particles with a lower density of matter.

For the coupling constant for interaction of nucleon and electron as gravitational monopoles in the field of strong gravitation we have:

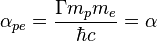\alpha_{pe}= \frac{ \Gamma m_p m_e }{\hbar c }= \alpha .

For the coupling constant for interaction of two electrons as gravitational monopoles in the field of strong gravitation we have:

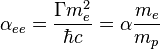\alpha_{ee}= \frac{ \Gamma m^2_e }{\hbar c }= \alpha \frac{m_e}{m_p}.

Since there is 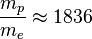~ \frac{m_p}{m_e}\approx 1836 , then the electromagnetic interaction of electrons 1836 times more of their strong gravitational interaction.

If the magnetic monopoles could exist in nature the energy of their magnetic interaction would be equal to:

U_m = \frac { q_m^2 }{4\pi \mu_0 r},

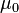where ~ \mu_0 is the vacuum permeability, ~ r is the distance between two magnetic charges.

The energy of photon is:

U_{ph} = \frac { hc }{\lambda}.

With condition 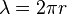~ \lambda = 2\pi r the magnetic coupling constant will be: [6]

\beta = \frac { U_m }{ U_{ph} } = \frac { q_m^2 }{4\pi \mu_0 \hbar c }= \frac{h}{2\mu_0 c e^2 }=\frac{1}{4\alpha } .

Stellar level

Charges and masses

In the theory of Infinite Hierarchical Nesting of Matter it is supposed that magnetars as a special class of neutron stars and stellar analogue of protons may have a certain electric charge: [7] [8]

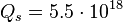Q_s = 5.5\cdot 10^{18} C.

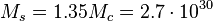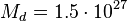The typical mass of magnetar is about ~M_{s}= 1.35 M_c=2.7\cdot 10^{30} kg. The mass of the discon – the analogue of the electron is: ~ M_d=1.5 \cdot 10^{27} kg or 250 Earth masses, or 0.78 Jupiter masses.

The stellar gravitational torsion flux quantum, as the velocity circulation quantum, is: 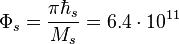\Phi_s = \frac{ \pi \hbar_s }{M_s} = 6.4 \cdot 10^{11} m2/s, where 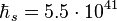~ \hbar_s= 5.5 \cdot 10^{41} J∙s is the stellar Dirac constant for the system with the magnetar.

The stellar magnetic flux quantum : 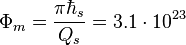\Phi_m = \frac{\pi \hbar_s } { Q_s } = 3.1\cdot 10^{23} J/A.

Stellar coupling constants

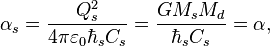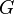The stellar fine structure constant is: ~ \alpha_s = \frac{ Q_s^2}{4 \pi \varepsilon_0 \hbar_s C_s }= \frac {G M_s M_d}{\hbar_s C_s }= \alpha , where ~ G is the gravitational constant, 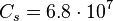~ C_s= 6.8 \cdot 10^{7} m/s is the stellar speed as the characteristic speed of the matter particles in a typical neutron star.

The coupling constant for interaction of two magnetars as gravitational monopoles is:

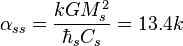\alpha_{ss}= \frac{ k G M^2_s }{ \hbar_s C_s }=13.4 k .

Due to SPФ symmetry and similarity of matter levels, the values of dimensionless constants are the same as at the level of atoms and on the level of stars.

See also

References

  1. ↑ Zhong, Fang at all. (2003). The Anomalous Hall Effect and Magnetic Monopoles in Momentum Space. Science 302 (5642) 92–95. doi:10.1126/science.1089408.
  2. ↑ Ville Pietilä, Mikko Möttönen, Creation of Dirac Monopoles in Spinor Bose–Einstein Condensates, Phys. Rev. Lett. 103, 030401 (2009).
  3. ↑ Stoney G. On The Physical Units of Nature, Phil.Mag. 11, 381–391, 1881.
  4. ↑ Paul Dirac, "Quantised Singularities in the Electromagnetic Field". Proc. Roy. Soc. (London) A 133, 60 (1931). Free web link
  5. ↑ Latest (2010) values of the constants.
  6. ↑ Yakymakha O.L., Kalnibolotskij Y.M. (1994). "Very-low-frequency resonance of MOSFET amplifier parameters". Solid- State Electronics 37(10),1739-1751. Pdf
  7. ↑ Fedosin S.G. Fizika i filosofiia podobiia: ot preonov do metagalaktik, Perm, (1999-06-09) 544 pp. ISBN 5-8131-0012-1.
  8. ↑ Sergey Fedosin, The physical theories and infinite hierarchical nesting of matter, Volume 1, LAP LAMBERT Academic Publishing, pages: 580, ISBN-13: 978-3-659-57301-9.
This article is issued from Wikiversity - version of the Thursday, February 12, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.