Momentum

Momentum, 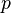$p$ is a vector quantity, or operator, which is defined in classical mechanics as the product of an object's mass, m, with its velocity $v$ .

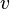Newton's second law, in its most general form, is written as:

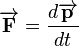
$\overrightarrow{\mathbf{F}} = \frac{d\overrightarrow{\mathbf{p}}}{dt}$

With this definition, we can find any change in momentum by rearranging this equation, and integrating on both sides:

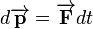
$d\overrightarrow{\mathbf{p}}=\overrightarrow{\mathbf{F}}dt$

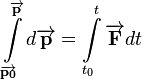
$\int\limits_{\overrightarrow{\mathbf{p_0}}}^{\overrightarrow{\mathbf{p}}}d\overrightarrow{\mathbf{p}} = \int\limits_{t_0}^{t} \overrightarrow{\mathbf{F}}dt$

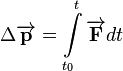
$\Delta\overrightarrow{\mathbf{p}}= \int\limits_{t_0}^{t} \overrightarrow{\mathbf{F}}dt$

The quantity 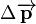$\Delta\overrightarrow{\mathbf{p}}$ is the impulse which is given the symbol 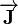$\overrightarrow{\mathbf{J}}$ . For a constant force, the integral on the right reduces to

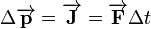
$\Delta\overrightarrow{\mathbf{p}}= \overrightarrow{\mathbf{J}} = \overrightarrow{\mathbf{F}}\Delta t$

In classical mechanics, momentum is defined to be the quantity 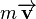$m\overrightarrow{\mathbf{v}}$ . If mass is constant, then it follows from Newton's second law that:

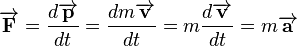
$\overrightarrow{\mathbf{F}} = \frac{d\overrightarrow{\mathbf{p}}}{dt} = \frac{dm\overrightarrow{\mathbf{v}}}{dt} = m\frac{d\overrightarrow{\mathbf{v}}}{dt} = m\overrightarrow{\mathbf{a}}$

An important law that is valid in all systems without any net external force acting, including relativistic, is that the total momentum of such a system must be conserved.

Note

In relativity theories, as well as in quantum mechanics, the momentum is derived from the classical concept, but it has more elaborate definitions than in Newtonian mechanics. In quantum physics the momentum and position operators are said to be complementary.

Relativistically momentum is defined as

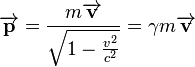
$\overrightarrow{\mathbf{p}} = \frac{m\overrightarrow{\mathbf{v}}}{\sqrt{1-\frac{v^2}{c^2}}} = \gamma m\overrightarrow{\mathbf{v}}$

for objects with mass; some mass-less elementary particles still have non-zero momentum.

This article is issued from Wikiversity - version of the Monday, March 11, 2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.