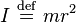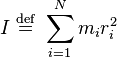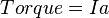Moments

The moment of inertia is sometimes called and referred to as "angular mass." It is the "amount of resistance" to changes in rotational motion.

The moment of inertia of a point mass m at a distance r from the axis of rotation is

I \ \stackrel{\mathrm{def}}{=}\ m r^2\,\!

The moment of inertia is additive, therefore, for a collection of 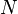$N$ point masses 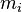$m_{i}$ with distances 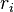$r_{i}$ to the rotation axis, the total moment of inertia is the sum of the point-mass moments of inertia

I \ \stackrel{\mathrm{def}}{=}\ \sum_{i=1}^{N} {m_{i} r_{i}^2}\,\!

The moment of inertia is commonly used to calculate torque when multiplied by the angular acceleration. This is analogous to F = ma.

Torque = Ia\,

This article is issued from Wikiversity - version of the Sunday, July 29, 2012. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.