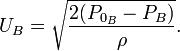Fluid Mechanics for MAP/Differential Analysis of Fluid Flow

< Fluid Mechanics for MAP

>back to Chapters of Fluid Mechanics for MAP

>back to Chapters of Microfluid Mechanics

Differential relations for a fluid particle

We are interested in the distribution of field properties at each point in space. Therefore, we analyze an infinitesimal region of a flow by applying the RTT to an infinitesimal control volume, or , to a infinitesimal fluid system.

Conservation of mass

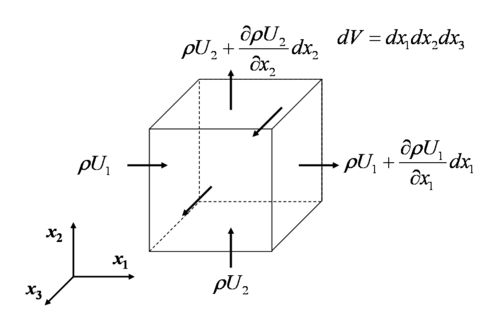
The differential control volume dV and the mass flux through its surfaces

The conservation of mass according to RTT

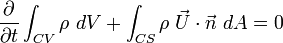
\displaystyle \frac{\partial}{\partial t}\int_{CV}\rho\ dV + \int_{CS}\rho\;\vec{U}\cdot\vec{n}\ dA = 0

or in tensor form

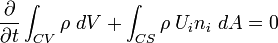
\displaystyle \frac{\partial}{\partial t}\int_{CV}\rho\ dV + \int_{CS}\rho\;U_i n_i\ dA = 0

The differential volume is selected to be so small that density 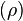$\displaystyle (\rho)$ can be accepted to be uniform within this volume. Thus the first integral in 1 is:

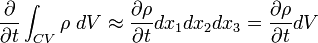
\displaystyle \frac{\partial}{\partial t}\int_{CV}\rho\ dV\approx\frac{\partial\rho}{\partial t}dx_{1}dx_{2}dx_{3}= \frac{\partial\rho}{\partial t}dV

The flux term (second integral term) in the equation of conservation of mass can be analyzed in groups:

\displaystyle \int_{CS}\rho U_i n_i\ dA = \int_{CS\,x_{1}} \rho U_i n_i\;dA + \int_{CS\,x_{2}} \rho U_i n_i\;dA + \int_{CS\,x_{3}} \rho U_i n_i\;dA

Let's look to the surfaces perpendicular to 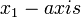$\displaystyle x_1-axis$

\displaystyle \int_{CS\, x_{1}}\rho U_i n_i\ dA = -\rho U_{1}dx_{2}dx_{3} + \left[\rho U_{1} + \frac{\partial\left(\rho U_{1}\right)}{\partial x_{1}}dx_{1}\right] dx_{2}dx_{3}

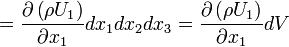
\displaystyle = \frac{\partial\left(\rho U_{1}\right)}{\partial x_{1}}dx_{1}dx_{2}dx_{3}= \frac{\partial\left(\rho U_{1}\right)}{\partial x_{1}}dV

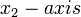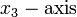Similarly, the flux integrals through surfaces perpendicular to $\displaystyle x_2-axis$ and $\displaystyle x_3-\textrm{axis}$ are

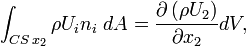
\displaystyle \int_{CS\,x_{2}}\rho U_i n_i\ dA = \frac{\partial\left(\rho U_{2}\right)}{\partial x_{2}}dV,

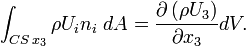
\displaystyle \int_{CS\,x_{3}}\rho U_i n_i\ dA = \frac{\partial\left(\rho U_{3}\right)}{\partial x_{3}}dV.

Hence the flux integral reads;

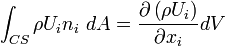
\displaystyle \int_{CS}\rho U_i n_i\ dA = \frac{\partial\left(\rho U_{i}\right)}{\partial x_{i}}dV

The conservation of mass equation becomes:

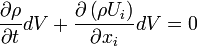
\displaystyle \frac{\partial \rho}{\partial t}dV + \frac{\partial\left(\rho U_{i}\right)}{\partial x_{i}}dV = 0

Droping the $\displaystyle dV$ , we reach to the final form of the conservation of mass:

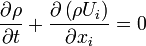
\displaystyle \frac{\partial \rho}{\partial t} + \frac{\partial\left(\rho U_{i}\right)}{\partial x_{i}} = 0

This equation is also called continuity equation. It can be written in vector form as:

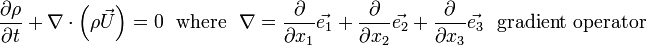
\displaystyle \frac{\partial \rho}{\partial t} + \nabla\cdot\left(\rho\vec{U}\right) = 0 \ \ \text{where} \ \ \nabla=\frac{\partial}{\partial x_{1}}\vec{e_{1}} + \frac{\partial}{\partial x_{2}}\vec{e_{2}} + \frac{\partial}{\partial x_{3}}\vec{e_{3}}\ \ \text{gradient operator}

For a steady flow, continuity equation becomes:

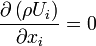
\displaystyle \frac{\partial\left(\rho U_{i}\right)}{\partial x_{i}} = 0

For incompresible flow, i.e. 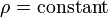$\displaystyle \rho=\text{constant}$ :

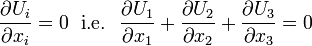
\displaystyle \frac{\partial U_{i}}{\partial x_{i}} = 0 \ \ \text{i.e.} \ \ \frac{\partial U_{1}}{\partial x_{1}} + \frac{\partial U_{2}}{\partial x_{2}} + \frac{\partial U_{3}}{\partial x_{3}}=0

Example

For a two dimensional, steady and incompressible flow in 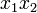$\displaystyle x_1 x_2$ plane given by:

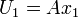
\displaystyle \displaystyle U_1=A x_1

Find how many possible 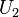$\displaystyle U_2$ can exist.

For incompressible steady flow:

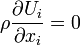
\displaystyle \rho\frac{\partial U_{i}}{\partial x_{i}} = 0

in two diemnsions

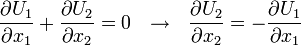
\displaystyle \frac{\partial U_{1}}{\partial x_{1}} + \frac{\partial U_{2}}{\partial x_{2}} =0 \ \ \rightarrow \ \ \frac{\partial U_{2}}{\partial x_{2}}=-\frac{\partial U_{1}}{\partial x_{1}}

Thus,

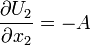
\displaystyle \frac{\partial U_{2}}{\partial x_{2}}=-A

This is an expression for the rate of change of 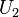$\displaystyle U_2$ velocity while keeping

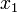$\displaystyle x_1$ constant. Therefore the integral of this equation reads

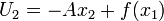
\displaystyle \displaystyle U_2=-Ax_2+f(x_1)

Thus, any function 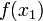$\displaystyle f(x_1)$ is allowable.

Example

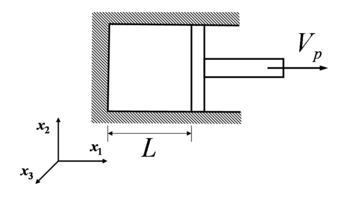
Compressible and unsteady flow inside a piston

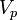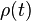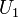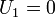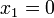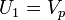Consider one-dimensional flow in the piston. The piston suddenly moves with the velocity $\displaystyle V_p$ . Assume uniform $\displaystyle \rho(t)$ in the piston and a linear change of velocity $\displaystyle U_1$ such that $\displaystyle U_1=0$ at the bottom ( $\displaystyle x_1=0$ ) and $\displaystyle U_1=V_p$ on the piston ( 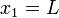$\displaystyle x_1=L$ ), i.e.

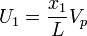
\displaystyle U_1=\frac{x_1}{L}V_p

Obtain a function for the density as a function of time.

The conservation of mass equation is:

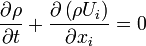
\displaystyle \frac{\partial \rho}{\partial t} + \frac{\partial\left(\rho U_{i}\right)}{\partial x_{i}} = 0

For one-dimensional flow and uniform $\displaystyle \rho$ , this equaiton simplifies to

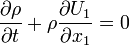
\displaystyle \frac{\partial \rho}{\partial t} + \rho\frac{\partial U_{1}}{\partial x_{1}} = 0

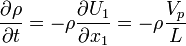
\displaystyle \frac{\partial \rho}{\partial t}=-\rho\frac{\partial U_{1}}{\partial x_{1}} = -\rho \frac{V_p}{L}

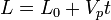
\displaystyle \displaystyle L=L_0+V_p t

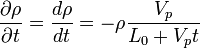
\displaystyle \frac{\partial \rho}{\partial t}=\frac{d\rho}{dt} = -\rho \frac{V_p}{L_0+V_p t}

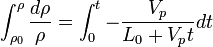
\displaystyle \int^{\rho}_{\rho_0}\frac{d\rho}{\rho} =\int^{t}_{0}-\frac{V_p}{L_0+V_pt}dt

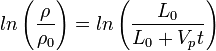
\displaystyle ln\left(\frac{\rho}{\rho_0}\right) =ln\left(\frac{L_0}{L_0+V_pt}\right)

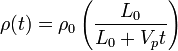
\displaystyle \rho(t)=\rho_0 \left(\frac{L_0}{L_0+V_pt}\right)

The same problem can be solved by using the integral approach with a deforming control volume.

The differential equation of linear momentum

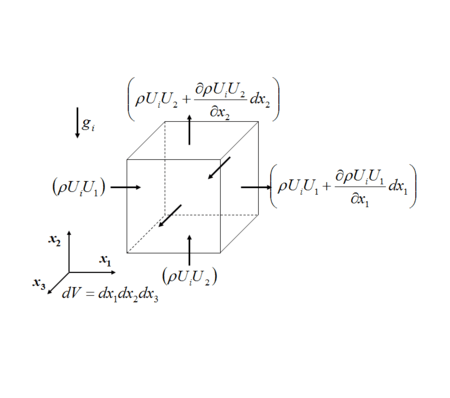
The differential control volume dV and the flux of

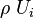\displaystyle \rho\;U_{i}

(momentum per unit volume in i-direction) through the surfaces perpendicular to

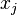\displaystyle x_{j}

axis

The integral equation for the momentum conservation is

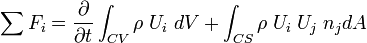
\displaystyle \sum F_{i} = \frac{\partial}{\partial t}\int_{CV} \rho\;U_{i}\;dV + \int_{CS}\rho\;U_{i}\;U_{j}\;n_{j}dA

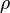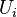For the first integral we assume $\displaystyle \rho$ and $\displaystyle U_{i}$ are uniform within dV, and dV is so small that:

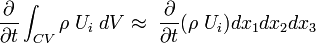
\displaystyle \frac{\partial}{\partial t}\int_{CV}\rho\;U_{i}\;dV \approx\ \frac{\partial}{\partial t}(\rho\;U_{i})dx_{1}dx_{2}dx_{3}

Analyze the flux of the 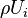$\displaystyle \rho U_i$ momentum terms through the faces perpendicular to the axis:

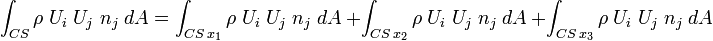
\displaystyle \int_{CS}\rho\;U_{i}\;U_{j}\;n_{j}\;dA = \int_{CS\,x_{1}}\rho\;U_{i}\;U_{j}\;n_{j}\;dA\ + \int_{CS\,x_{2}}\rho\;U_{i}\;U_{j}\;n_{j}\;dA\ + \int_{CS\,x_{3}}\rho\;U_{i}\;U_{j}\;n_{j}\;dA

First consider the flux of 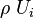$\displaystyle \rho\;U_{i}$ (momentum per unit volume in i-direction) through the surfaces perpendicular to 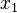$\displaystyle x_{1}$ axis:

\displaystyle \int_{CS\,x_{1}}\rho\;U_{i}\;U_{j}\;n_{j}\;dA = -\rho\;U_{i}\;U_{1}\;dx_{2}dx_{3}\; + \left[\rho\ U_{i}\ U_{1}\ dx_{2}\ dx_{3} + \frac{\partial}{\partial x_{1}}(\rho\ U_{i}\ U_{1})\ dx_{1}\right]dx_{2}\ dx_{3}

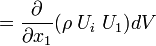
\displaystyle = \frac{\partial}{\partial x_{1}}(\rho\;U_{i}\;U_{1})dV

Similarly, the momentum flux through the surfaces in other directions read

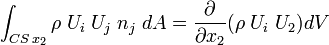
\displaystyle \int_{CS\,x_{2}}\rho\;U_{i}\;U_{j}\;n_{j}\;dA = \frac{\partial}{\partial x_{2}}(\rho\;U_{i}\;U_{2})dV

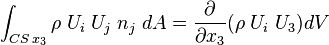
\displaystyle \int_{CS\,x_{3}}\rho\;U_{i}\;U_{j}\;n_{j}\;dA = \frac{\partial}{\partial x_{3}}(\rho\;U_{i}\;U_{3})dV

Rearranging the equation for 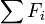$\displaystyle \sum F_{i}$ we obtain:

\displaystyle \sum F_{i} = \left[\frac{\partial}{\partial t}(\rho\ U_{i}) + \frac{\partial}{\partial x_{j}}(\rho\ U_{i}\ U_{j})\right]dV

We can simplify further:

\displaystyle \sum F_{i} = \left[U_{i}\frac{\partial \rho}{\partial t} + \rho\frac{\partial U_{i}}{\partial t} + U_{i} \frac{\partial}{\partial x_{j}}(\rho\;U_{j}) + \rho\;U_{j}\;\frac{\partial U_{i}}{\partial x_{j}}\right]dV

\displaystyle \sum F_{i}= U_{i}\underbrace{\left[\frac{\partial \rho}{\partial t}\;+ \frac{\partial}{\partial x_{j}}(\rho\;U_{j})\right]}_{continuity\ equation=0}dV\;+ \rho\underbrace{\left[\frac{\partial U_{i}}{\partial t}\;+ U_{j}\frac{\partial U_{i}}{\partial x_{j}}\right]}_{\frac{D U_{i}}{D t};subtantial\ derivative\ of\ U_i}dV

Hence

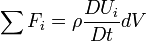
\displaystyle \sum F_{i} = \rho\frac{D U_{i}}{D t} dV

Let's look to the forces on the exposed on the diffrential control volume:

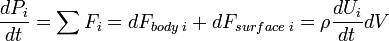
\displaystyle \frac{dP_{i}}{dt} = \sum F_{i} = dF_{body\;i} + dF_{surface\;i} = \rho \frac{dU_{i}}{dt}dV

Here, only gravitational force is considered as a body force. Thus,

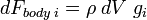
\displaystyle dF_{body\;i} = \rho\;dV\;g_{i}

Differential surface forces

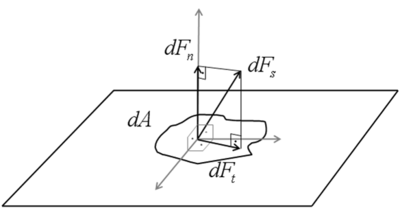
Surface forces are the stresses acting on the control surfaces. 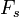$\displaystyle F_{s}$ can be resolved into three components. 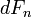$\displaystyle dF_{n}$ is normal to dA. 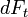$\displaystyle dF_{t}$ are tangent to dA:

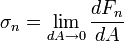
\displaystyle \sigma_{n} = \lim_{d A\rightarrow 0} \frac{d F_{n}}{d A}

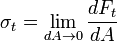
\displaystyle \sigma_{t} = \lim_{d A\rightarrow 0} \frac{d F_{t}}{d A}

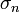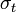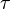$\displaystyle \sigma_{n}$ is a normal stress whereas $\displaystyle \sigma_{t}$ is a shear stress. The shear stresses are also designated by $\displaystyle \tau$ .

Stresses on the surface of differential control volume

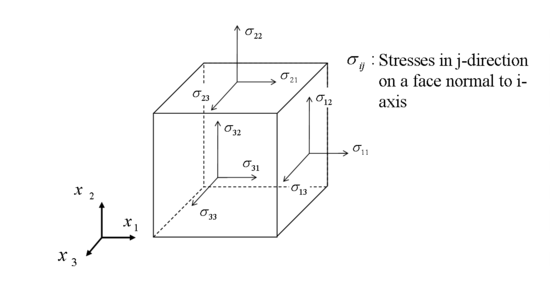
Thus, the surface forces are due to stresses on the surfaces of the control surface.

\displaystyle \sigma_{ij}=\left[ \begin{matrix} \sigma_{11} & \sigma_{12} & \sigma_{13} \\ \sigma_{21} & \sigma_{22} & \sigma_{23} \\ \sigma_{31} & \sigma_{32} & \sigma_{33} \end{matrix} \right]

The positive stress directions

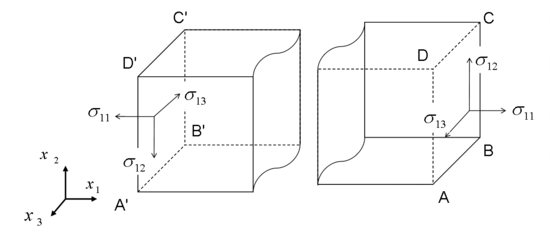
We define the positive direction for the stress as the positive coordinate direction on the surfaces (e.g. on ABCD) for which the outwards normal is in the positive coordinate direction . If the outward normal represents the negative direction (A'B'C'D'), then the stresses are considered positive if directed in the negative coordinate directions.

The stresses on the surface 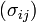$\displaystyle (\sigma_{ij})$ are the sum of pressure plus the viscous stresses which arise from motion with velocity gradients:

\displaystyle \sigma_{ij}=\left[ \begin{matrix} -P & 0 & 0 \\ 0 & -P & 0 \\ 0 & 0 & -P \end{matrix} \right] + \left[ \begin{matrix} \tau_{11} & \tau_{12} & \tau_{13} \\ \tau_{21} & \tau_{22} & \tau_{23} \\ \tau_{31} & \tau_{32} & \tau_{33} \end{matrix} \right]= \left[ \begin{matrix} -P+\tau_{11} & \tau_{12} & \tau_{13} \\ \tau_{21} & -P+\tau_{22} & \tau_{23} \\ \tau_{31} & \tau_{32} & -P+\tau_{33} \end{matrix} \right]

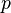$\displaystyle p$ has a minus sign since the force due to pressure acts opposite to the surface normal.

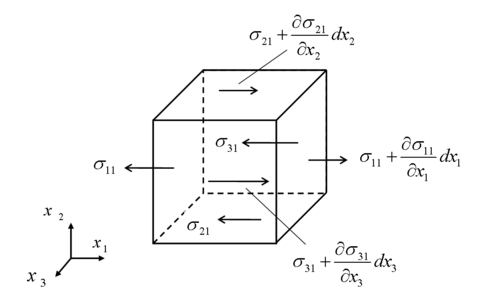
Stresses on the surface of the differential control volume in the x1 direction

Let us look to the differential surface force in the 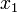$\displaystyle x_1$ direction:

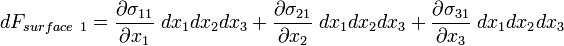
\displaystyle dF_{surface\ 1} = \frac{\partial\sigma_{11}}{\partial x_{1}}\;dx_{1}dx_{2}dx_{3} + \frac{\partial\sigma_{21}}{\partial x_{2}}\;dx_{1}dx_{2}dx_{3} + \frac{\partial\sigma_{31}}{\partial x_{3}}\;dx_{1}dx_{2}dx_{3}

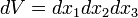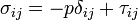Noting that $\displaystyle dV=dx_{1}dx_{2}dx_{3}$ and $\displaystyle \sigma_{ij}=-p\delta_{ij}+\tau_{ij}$ (4),

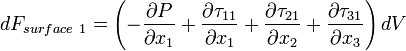
\displaystyle dF_{surface\ 1} = \left(-\frac{\partial P}{\partial x_{1}} + \frac{\partial\tau_{11}}{\partial x_{1}} + \frac{\partial\tau_{21}}{\partial x_{2}} + \frac{\partial\tau_{31}}{\partial x_{3}}\right)dV

Thus in tensor form the differential surface forces in 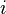$\displaystyle i$ 'th direction can be written as

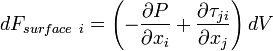
\displaystyle dF_{surface\ i} = \left(-\frac{\partial P}{\partial x_{i}} + \frac{\partial\tau_{ji}}{\partial x_{j}}\right)dV

Note that 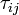$\displaystyle \tau_{ij}$ is a symmetric tensor, i.e.

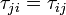
\displaystyle \tau_{ji}=\tau_{ij}

Hence, the diffential surface forces reads:

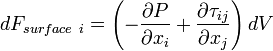
\displaystyle dF_{surface\ i} = \left(-\frac{\partial P}{\partial x_{i}} + \frac{\partial\tau_{ij}}{\partial x_{j}}\right)dV

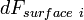Inserting $\displaystyle dF_{body\ i}$ and $\displaystyle dF_{surface\ i}$ into (2),

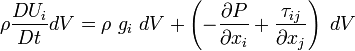
\displaystyle \rho \frac{DU_{i}}{Dt}dV = \rho\ g_{i}\ dV + \left(-\frac{\partial P}{\partial x_{i}} + \frac{\tau_{ij}}{\partial x_{j}}\right)\;dV

and canceling 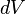$\displaystyle dV$ we obtain

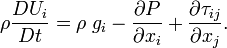
\displaystyle \rho \frac{DU_{i}}{Dt} = \rho\;g_{i} -\frac{\partial P}{\partial x_{i}} + \frac{\partial \tau_{ij}}{\partial x_{j}}.

Expanding the substatial derivative at the left hand side,

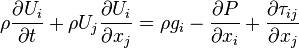
\displaystyle \rho\frac{\partial U_{i}}{\partial t} + \rho U_{j}\frac{\partial U_{i}}{\partial x_{j}} = \rho g_{i} -\frac{\partial P}{\partial x_{i}} + \frac{\partial \tau_{ij}}{\partial x_{j}}

We obtain the the most general form of momentum equation which is valid for any fluid (Newtonian, Non-newtonian, Compressible, etc.). It is non-linear due to the 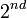$\displaystyle 2^{nd}$ term at the LHS. Efect of Newtonian and Non-newtonian properties appears in the formulation of the viscous stresses 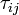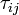$\displaystyle \tau_{ij}$ . $\displaystyle \tau_{ij}$ will introduce also non-linearity when the fluid is non-Newtonian.

It should be noted that these formulations are based on stress conception which was thought to exist in fluids in motion. However it is known that 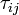$\displaystyle \tau_{ij}$ can be expressed as momentum transfer per unit area and time. Thus it can be considered as molecular momentum transport term. Derivations based on this concept requires a molecular approach (which is lengthy). The students should be aware that 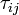$\displaystyle \tau_{ij}$ causes momentum transport when there is a gradient of velocity.

Linear momentum equation for Newtonian Fluid: "Navier-Stokes Equation"

For a Newtonian fluid, the viscous stresses are defined as:

\displaystyle \tau_{ij} = \mu\left[\frac{\partial U_{i}}{\partial x_{j}} + \frac{\partial U_{j}}{\partial x_{i}}\right] - \frac{2}{3}\delta_{ij}\mu\frac{\partial U_{k}}{\partial x_{k}}

Note that derivation of this relation is beyond the scaope of this course.

Thus, the momentum equation (6) becomes

\displaystyle \rho\frac{DU_{i}}{Dt} = \rho g_{i} - \frac{\partial P}{\partial x_{i}} + \frac{\partial}{\partial x_{j}}\left[\mu \left(\frac{\partial U_{i}}{\partial x_{j}} + \frac{\partial U_{j}}{\partial x_{i}}\right) - \frac{2}{3}\mu\ \delta_{ij}\ \frac{\partial U_{k}}{\partial x_{k}}\right]

For a flow with constant viscosity (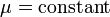 $\displaystyle \mu=\textrm{constant}$ ):

\displaystyle \rho\frac{DU_{i}}{Dt} = \rho g_{i} - \frac{\partial P}{\partial x_{i}} + \mu \frac{\partial}{\partial x_{j}}\left[\frac{\partial U_{i}}{\partial x_{j}} + \frac{\partial U_{j}}{\partial x_{i}} - \frac{2}{3}\delta_{ij}\ \frac{\partial U_{k}}{\partial x_{k}}\right]

since,

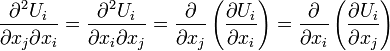
\displaystyle \frac{\partial^{2}U_{i}}{\partial x_{j}\partial x_{i}} = \frac{\partial^{2}U_{i}}{\partial x_{i}\partial x_{j}} = \frac{\partial}{\partial x_{j}}\left(\frac{\partial U_{i}}{\partial x_{i}}\right) = \frac{\partial}{\partial x_{i}}\left(\frac{\partial U_{i}}{\partial x_{j}}\right)

then,

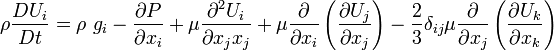
\displaystyle \rho\frac{DU_{i}}{Dt} = \rho\ g_{i} -\frac{\partial P}{\partial x_{i}} + \mu \frac{\partial^{2} U_{i}}{\partial x_{j}x_{j}} + \mu\frac{\partial}{\partial x_{i}}\left(\frac{\partial U_{j}}{\partial x_{j}}\right) - \frac{2}{3}\delta_{ij}\mu\frac{\partial}{\partial x_j}\left(\frac{\partial U_{k}}{\partial x_{k}}\right)

For an incompressible flow

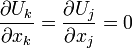
\displaystyle \frac{\partial U_{k}}{\partial x_{k}} = \frac{\partial U_{j}}{\partial x_{j}} = 0

hence assuming that the viscosity is constant, it can be easily shown that the momentum equation reduces to

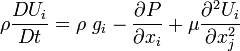
\displaystyle \rho\frac{DU_{i}}{Dt} = \rho\ g_{i} -\frac{\partial P}{\partial x_{i}} + \mu\frac{\partial^{2}U_{i}}{\partial x_{j}^{2}}

Euler's equation: Inviscid flow

When the velocity gradients in the flow is negligible and/or the Reynolds number takes very high values, the viscous stresses can be neglected:

\displaystyle \displaystyle \tau_{ij} = 0

Since, the viscous stresses are proportional to viscosity:

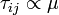
\displaystyle \tau_{ij} \propto \mu

for flows, where 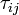$\displaystyle \tau_{ij}$ is neglected, the flow is called frictionless or inviscid, although there is a finite viscosity of the flow. Accordingly, the linear momentum equation reduces to

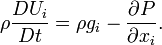
\displaystyle \rho\frac{DU_{i}}{Dt} = \rho g_{i} -\frac{\partial P}{\partial x_{i}}.

Euler's equation in streamline coordinates

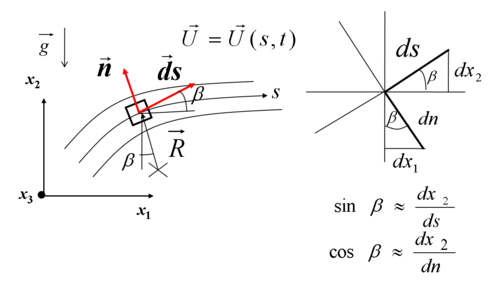
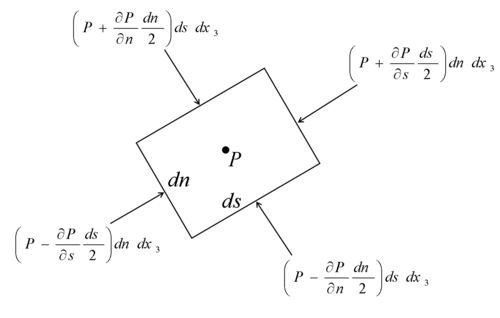
Differential control volume along streamline coordinates and the forces on it for a inviscid flow

Differential control volume along streamline coordinates and the forces on it for a inviscid flow

Euler's equation take a special form along and normal to a streamline with which one can see the dependency between the pressure, velocity and curvature of the streamline.

To obtain Euler's equation in s-direction, apply Newton's second law in s-direction in the absence of viscous forces.

\displaystyle \rho dV \left[\frac{\partial U_{s}}{\partial t} + U_{s}\frac{\partial U_{s}}{\partial s}\right]= -\frac{\partial P}{\partial s}dV -\rho\ gsin\beta dV

Omitting 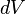$\displaystyle dV$ would deliver

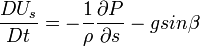
\displaystyle \frac{DU_{s}}{Dt}= -\frac{1}{\rho}\frac{\partial P}{\partial s} - gsin\beta

Since

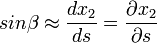
\displaystyle sin\beta \approx \frac{d x_{2}}{d s}=\frac{\partial x_{2}}{\partial s}

then the Equler's equation along a streamline reads

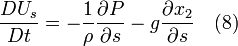
\displaystyle \frac{DU_{s}}{Dt}= -\frac{1}{\rho}\frac{\partial P}{\partial s} - g\frac{\partial x_{2}}{\partial s}\ \ \ (8)

For a steady flow and by neglecting body forces,

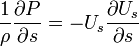
\displaystyle \frac{1}{\rho}\frac{\partial P}{\partial s} = -U_{s}\frac{\partial U_{s}}{\partial s}

it can be seen that decrease in velocity means increase in pressure as is indicated by the Bernoulli equation.

To obtain Euler's equation in n direction, apply Newton's second law in the absence of viscous forces and for a steady flow.

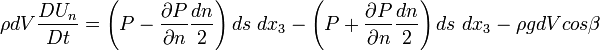
\displaystyle \rho dV\frac{DU_{n}}{Dt}= \left(P-\frac{\partial P}{\partial n}\frac{dn}{2}\right)ds\ dx_{3} - \left(P + \frac{\partial P}{\partial n}\frac{dn}{2}\right)ds\ dx_{3} - \rho g dV cos\beta

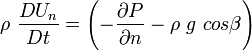
\displaystyle \rho\ \frac{DU_{n}}{Dt}=\left(-\frac{\partial P}{\partial n} - \rho\ g\ cos\beta\right)

Since,

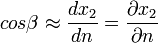
\displaystyle cos\beta \approx \frac{d x_{2}}{d n}=\frac{\partial x_{2}}{\partial n}

Then,

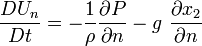
\displaystyle \frac{DU_{n}}{Dt}=-\frac{1}{\rho}\frac{\partial P}{\partial n} - g\ \frac{\partial x_{2}}{\partial n}

For a steady flow, the normal acceleration of the fluid is towards the center of curvature of the streamline:

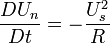
\displaystyle \frac{DU_{n}}{Dt} = -\frac{U_{s}^{2}}{R}

Hence,

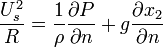
\displaystyle \frac{U_{s}^{2}}{R}=\frac{1}{\rho}\frac{\partial P}{\partial n} + g\frac{\partial x_{2}}{\partial n}

For an unsteady flow,

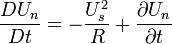
\displaystyle \frac{DU_{n}}{Dt} = -\frac{U_{s}^{2}}{R} + \frac{\partial U_{n}}{\partial t}

For steady flow neglecting body forces, the Euler's equation normal to the streamline is

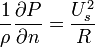
\displaystyle \frac{1}{\rho}\frac{\partial P}{\partial n} = \frac{U_{s}^{2}}{R}

which indicates that pressure increases in a direction outwards from the center of the curvature of the streamlines. In other words, pressure drops towards the center of curvature, which, consequently creates a potential difference in terms of pressure and forces the fluid to change its direction. For a straight streamline $\displaystyle R\rightarrow \infty$ , there is no pressure variation normal to the streamline.

Bernoulli equation: Integration of Euler's equation along a streamline for a steady flow

For a steady flow, Euler's equation along a streamline reads,

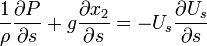
\displaystyle \frac{1}{\rho}\frac{\partial P}{\partial s} + g\frac{\partial x_{2}}{\partial s} = -U_{s}\frac{\partial U_{s}}{\partial s}

If a fluid particle moves a distance ds, along a streamline, since every variable becomes a function of $\displaystyle s$ :

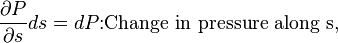
\displaystyle \frac{\partial P}{\partial s}ds = d P \text{:Change in pressure along s,}

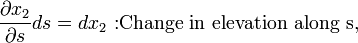
\displaystyle \frac{\partial x_{2}}{\partial s}ds = dx_{2}\ \text{:Change in elevation along s,}

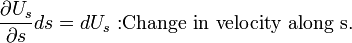
\displaystyle \frac{\partial U_{s}}{\partial s}ds = dU_{s}\ \text{:Change in velocity along s.}

Integration of the Euler equation between two locations, 1 and 2, along $\displaystyle s$ reads

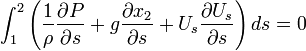
\displaystyle \int_{1}^{2} \left({\frac{1}{\rho}\frac{\partial P}{\partial s} + g\frac{\partial x_{2}}{\partial s}+U_{s}\frac{\partial U_{s}}{\partial s}}\right)ds=0

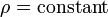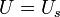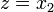For incompressible flow $\displaystyle \rho = \textrm{constant}$ and after changing the notation as: $\displaystyle U=U_{s}$ and $\displaystyle z=x_{2}$ , the integration results in

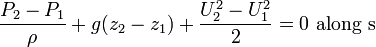
\displaystyle \frac{P_2-P_1}{\rho} + g(z_2-z_1) + \frac{U_2^{2}-U_1^{2}}{2} = 0 \textrm{\ along\ s}

or in its most beloved form:

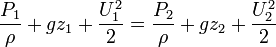
\displaystyle \frac{P_1}{\rho} + g z_1 + \frac{U_1^{2}}{2} = \frac{P_2}{\rho} + gz_2 + \frac{U_2^{2}}{2}

In other words along a streamline:

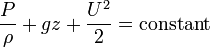
\displaystyle \frac{P}{\rho} + gz + \frac{U^{2}}{2} = \textrm{constant}

Note that due to the assumptions made during the derivation, the following restrictions applies to this equation: The flow should be steady, incompressible, frictionless and the equation is valid only along a streamline.

Different forms of Bernoulli equation

The common forms of Bernoulli equation are as follows:

Energy form (per unit mass)

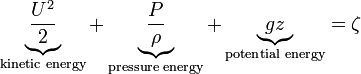
\displaystyle \underbrace{\frac{U^{2}}{2}}_{\text{kinetic energy}} + \underbrace{\frac{P}{\rho}}_{\text{pressure energy}} + \underbrace{gz}_{\text{potential energy}} = \zeta

Pressure form

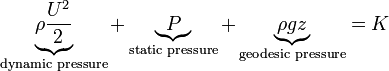
\displaystyle \underbrace{\rho\frac{U^{2}}{2}}_{\text{dynamic pressure}} + \underbrace{P}_{\text{static pressure}} + \underbrace{\rho gz}_{\text{geodesic pressure}} = K

Head form

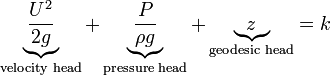
\displaystyle \underbrace{\frac{U^{2}}{2g}}_{\text{velocity head}} + \underbrace{\frac{P}{\rho g}}_{\text{pressure head}} + \underbrace{z}_{\text{geodesic head}} = k

Static, stagnation and dynamic pressures

How do we measure pressure? When the streamlines are parallel to the wall we can use pressure taps.

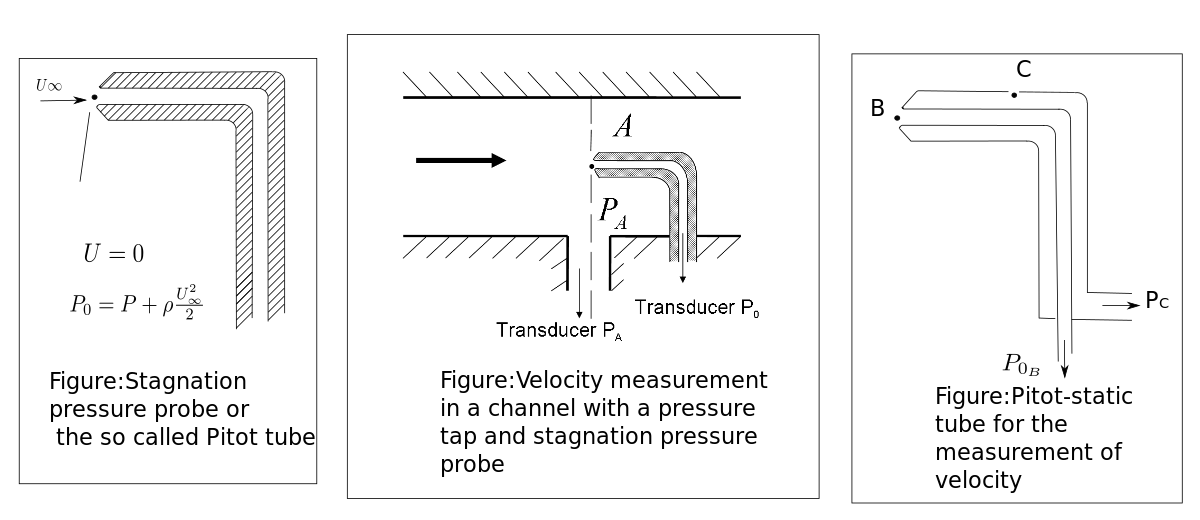
If the measured location is far from the wall, static pressure measurements can be made by a static pressure probe.

The stagnation pressure is the value obtained when a flowing fluid is decelerated to zero velocity by a frictionless flow process. The Stagnation pressure can be calculated as follows: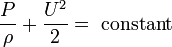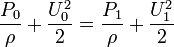

\displaystyle \frac{P}{\rho} + \frac{U^{2}}{2} =\;\textrm{constant}

\displaystyle \frac{P_{0}}{\rho} + \frac{U^{2}_{0}}{2} = \frac{P_{1}}{\rho} + \frac{U^{2}_{1}}{2}

when $\displaystyle U^{2}_{0} = 0$

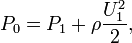
\displaystyle P_{0} = P_{1} + \rho\frac{U^{2}_{1}}{2},

where the last term is the dynamic pressure.

Pitot tube used in racing car

Figure: a)Jet is impinging to the wall and stagnating at the point of impingment b)Schematics of a of a pressure tap in a channel c)Static pressure probe

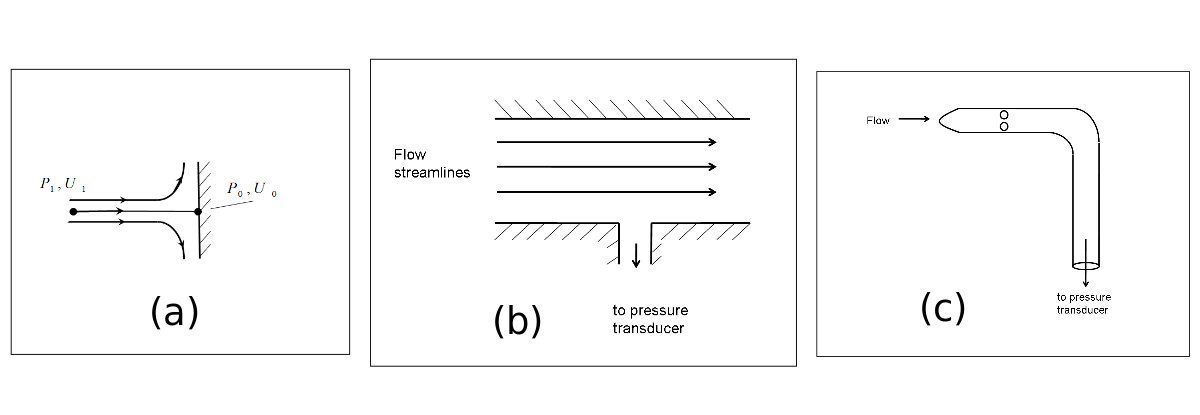
If we know the pressure difference 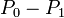$\displaystyle P_{0} - P_{1}$ , we can calculate the 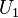$\displaystyle U_{1}$ velocity.

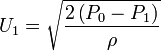
\displaystyle U_{1} = \sqrt{\frac{2\left(P_{0}-P_{1}\right)}{\rho}}

The stagnation pressure is measured in the laboratory using a probe that faces directly upstream flow.

Such a probe is called a stagnation pressure probe or Pitot tube . Thus, using a pressure tap and a Pitot tube one can measure local velocity:

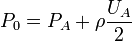
\displaystyle P_{0} = P_{A} + \rho\frac{U_{A}}{2}

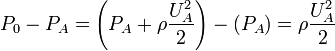
\displaystyle P_{0} - P_{A} = \left(P_{A} + \rho\frac{U^{2}_{A}}{2}\right) - (P_{A}) = \rho\frac{U^{2}_{A}}{2}

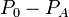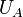Thus, measuring $\displaystyle P_{0} - P_{A}$ one can determine $\displaystyle U_A$ .

Pitot-static tube for velocity measurement

However, in the absence of a wall with well defined location, the velocity can be measured by a Pitot-static tube. The pressure is measured at B and C; assuming $\displaystyle P_{B} = P_{C}$ .

Hence,

$\displaystyle U_{B} = \sqrt{\frac{2(P_{0_B}-P_{B})}{\rho}}.$

Unsteady Bernoulli equation

The Euler's equation along a streamline is:

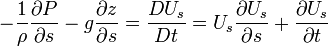
\displaystyle -\frac{1}{\rho}\frac{\partial P}{\partial s} - g\frac{\partial z}{\partial s} = \frac{DU_{s}}{Dt} = U_{s}\frac{\partial U_{s}}{\partial s} + \frac{\partial U_{s}}{\partial t}

along ds,

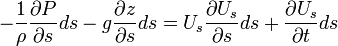
\displaystyle -\frac{1}{\rho}\frac{\partial P}{\partial s}ds - g\frac{\partial z}{\partial s}ds = U_{s}\frac{\partial U_{s}}{\partial s}ds + \frac{\partial U_{s}}{\partial t}ds

hence,

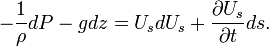
\displaystyle -\frac{1}{\rho}dP - gdz = U_{s}dU_{s} + \frac{\partial U_{s}}{\partial t}ds.

Integration between two points along a streamline is:

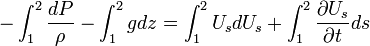
\displaystyle -\int^{2}_{1}{\frac{dP}{\rho}} - \int^{2}_{1}{g}dz = \int^{2}_{1}{U_{s}dU_{s}} + \int^{2}_{1}{\frac{\partial U_{s}}{\partial t}}ds

For incompressible flow, 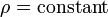$\displaystyle \rho = \textrm{constant}$ , thus the integral reads

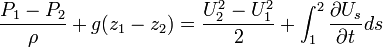
\displaystyle \frac{P_{1}-P_{2}}{\rho} + g(z_{1}- z_{2}) = \frac{U^{2}_{2}-U^{2}_{1}}{2} + \int^{2}_{1}{\frac{\partial U_{s}}{\partial t}ds}

The unsetady Bernoulli equation involves the integration of the time gradient of the velocity between two points.:

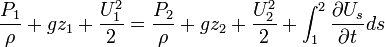
\displaystyle \frac{P_{1}}{\rho} + gz_{1} + \frac{U^{2}_{1}}{2} = \frac{P_{2}}{\rho} + gz_{2} + \frac{U^{2}_{2}}{2} + \int^{2}_{1}{\frac{\partial U_{s}}{\partial t}ds}

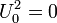
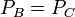This article is issued from Wikiversity - version of the Tuesday, February 09, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.