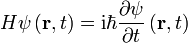Materials Science and Engineering/Equations/Quantum Mechanics
< Materials Science and Engineering < EquationsRelation between energy and frequency of a quanta of radiation
- Energy:

- Frequency:

- Angular Frequency:
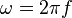
- Wavenumber:
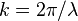
- Plank's Constant:
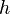
De Broglie Hypothesis
- Wavelength:
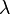
- Momentum:
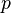
Phase of a Plane Wave Expressed as a Complex Phase Factor
Time-Dependent Schrodinger Equation
- Ket:
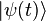
- Reduced Planck's Constant:
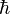
- Hamiltonian:
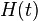
- The Hamiltonian describes the total energy of the system.
- Partial Derivative:
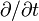
- Mass:
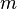
- Potential:
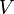
Derivation
Begin with a step from the time-independent derivation
Set each side equal to a constant, 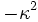
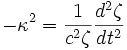
Multiply by 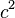 to remove constants on the right side of the equation.
to remove constants on the right side of the equation.
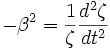
The solution is similar to what was found previously
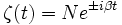
The amplitude at a point 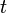 is equal to the amplitude at a point
is equal to the amplitude at a point 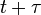
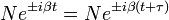
The following equation must be true:
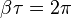
Rewrite 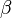 in terms of the frequency
in terms of the frequency
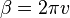
Enter the equation into the expression of 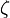
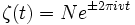
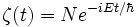
The time-dependent Schrodinger equation is a product of two 'sub-functions'
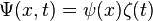
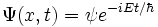
To extract  , differentiate with respect to time:
, differentiate with respect to time:
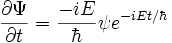
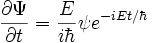
Rearrange:
Time-Independent Schrodinger Equation
- Del Operator:
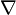
Derivation
The Schrodinger Equation is based on two formulas:
- The classical wave function derived from the Newton's Second Law
- The de Broglie wave expression
Formula of a classical wave:
Separate the function into two variables:
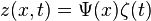
Insert the function into the wave equation:
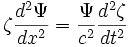
Rearrange to separate 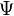 and
and 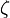
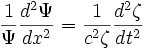
Set each side equal to an arbitrary constant, 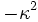
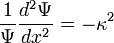
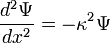
Solve this equation
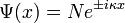
The amplitude at one point needs to be equal to the amplitude at another point:
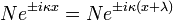
The following condition must be true:
Incorporate the de Broglie wave expression
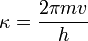
Use the symbol 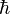
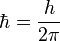
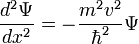
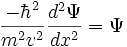
Use the expression of kinetic energy, 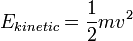
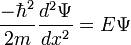
Modify the equation by adding a potential energy term and the Laplacian operator
Non-Relativistic Schrodinger Wave Equation
In non-relativistic quantum mechanics, the Hamiltonian of a particle can be expressed as the sum of two operators, one corresponding to kinetic energy and the other to potential energy. The Hamiltonian of a particle with no electric charge and no spin in this case is:
- kinetic energy operator:
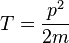
- mass of the particle:
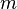
- momentum operator:
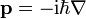
- potential energy operator:
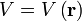
- real scalar function of the position operator
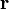 :
: 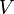
- Gradient operator:
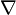
- Laplace operator:
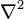
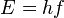
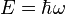
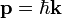
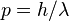
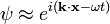
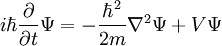

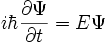


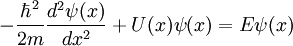
![\left[-\frac{\hbar^2}{2 m} \nabla^2 + U(\mathbf{r}) \right] \psi (\mathbf{r}) = E \psi (\mathbf{r})](../I/m/04b46a8810d1428aaac76caf376c980d.png)
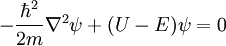
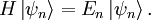
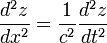
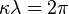
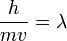
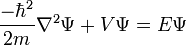
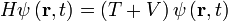
![H \psi\left(\mathbf{r}, t\right) = \left[ - \frac{\hbar^2}{2m} \nabla^2 + V\left(\mathbf{r}\right) \right] \psi\left(\mathbf{r}, t\right)](../I/m/664043a0fe95bd917ea67d5a02b3cf63.png)