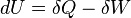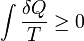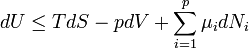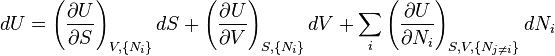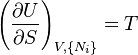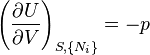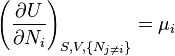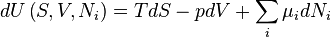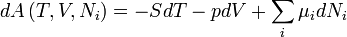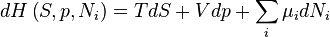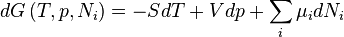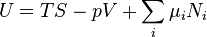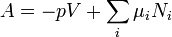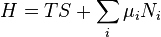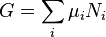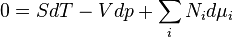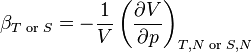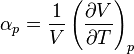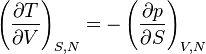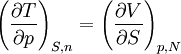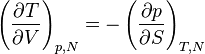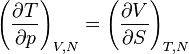Materials Science and Engineering/Equations
< Materials Science and EngineeringNotation
| Conjugate variables | |||
|---|---|---|---|
| p | Pressure | V | Volume |
| T | Temperature | S | Entropy |
| μ | Chemical potential | N | Particle number |
| Thermodynamic potentials | |||
|---|---|---|---|
| U | Internal energy | A | Helmholtz free energy |
| H | Enthalpy | G | Gibbs free energy |
| Material properties | |
|---|---|
| ρ | Density |
| CV | Heat capacity (constant volume) |
| Cp | Heat capacity (constant pressure) |
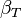 | Isothermal compressibility |
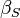 | Adiabatic compressibility |
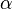 | Coefficient of thermal expansion |
| Other conventional variables | |
|---|---|
| δw | infinitesimal amount of Mechanical Work |
| δq | infinitesimal amount of Heat |
| Constants | |
|---|---|
| kB | Boltzmann constant |
| R | Ideal gas constant |
Equations
Laws of Thermodynamics
First Law of Thermodynamics:
Second Law of Thermodynamics:
Fundamental Equations
The Fundamental Equation:
The equation may be seen as a particular case of the chain rule:
from which the following identifications can be made:
These equations are known as "equations of state" with respect to the internal energy.
Thermodynamic Potentials
Thermodynamic Potentials:
Name Formula Natural variables Internal energy 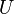
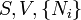
Helmholtz free energy 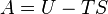
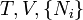
Enthalpy 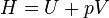
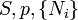
Gibbs free energy 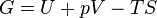
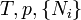
For the above four potentials, the fundamental equations are expressed as:
Euler Integrals:
Because all of natural variables of the internal energy U are extensive quantities, it follows from Euler's homogeneous function theorem that
Substituting into the expressions for the other main potentials we have the following expressions for the thermodynamic potentials:
Note that the Euler integrals are sometimes also referred to as fundamental equations.
Gibbs Duhem Relationship:
Differentiating the Euler equation for the internal energy and combining with the fundamental equation for internal energy, it follows that:
which is known as the Gibbs-Duhem relationship. The Gibbs-Duhem is a relationship among the intensive parameters of the system. It follows that for a simple system with r components, there will be r+1 independent parameters, or degrees of freedom. For example, a simple system with a single component will have two degrees of freedom, and may be specified by only two parameters, such as pressure and volume for example. The law is named after Josiah Gibbs and Pierre Duhem.
Materials Properties
Compressibility: At constant temperature or constant entropy
Heat Capacity at Constant Pressure:
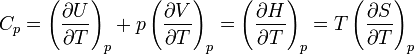
Heat Capacity at Constant Volume:
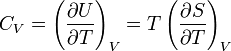
Coefficient of Thermal Expansion:
Maxwell Relations:
Maxwell relations are equalities involving the second derivatives of thermodynamic potentials with respect to their natural variables. They follow directly from the fact that the order of differentiation does not matter when taking the second derivative. The four most common Maxwell relations are:
Processes
Incremental Processes:
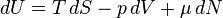
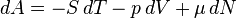
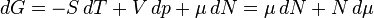
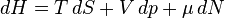 Equation Table for an Ideal Gas (
Equation Table for an Ideal Gas (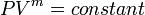 ):
):
| Constant Pressure | Constant Volume | Isothermal | Adiabatic | |
| Variable | 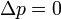 |
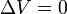 |
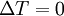 |
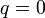 |
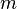 |
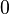 |
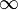 |
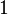 |
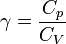 |
Work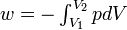 |
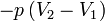 |
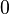 |
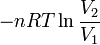 |
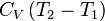 |
Heat Capacity, 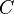 |
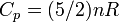 |
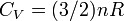 |
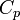 or or 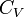 |
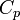 or or 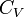 |
Internal Energy, 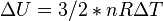 |
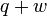 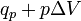 |
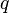 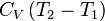 |
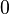 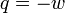 |
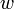 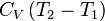 |
Enthalpy, 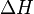 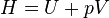 |
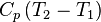 |
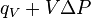 |
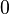 |
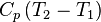 |
Entropy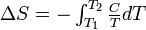 |
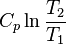 |
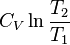 |
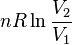 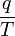 |
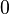 |