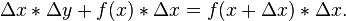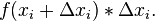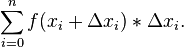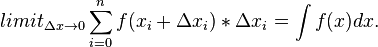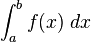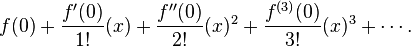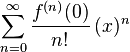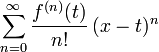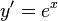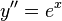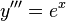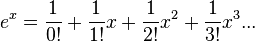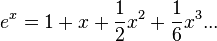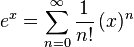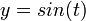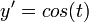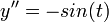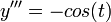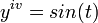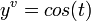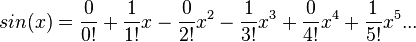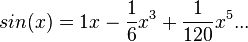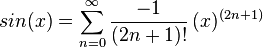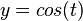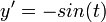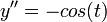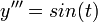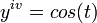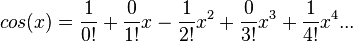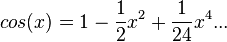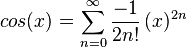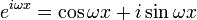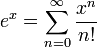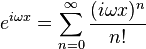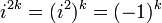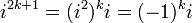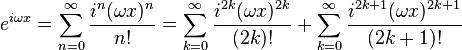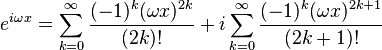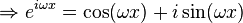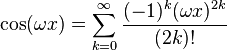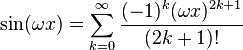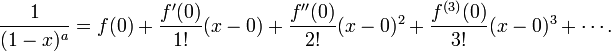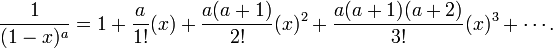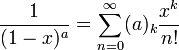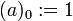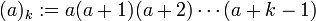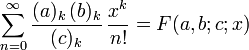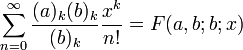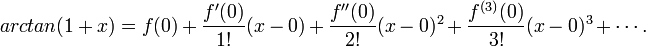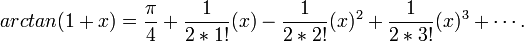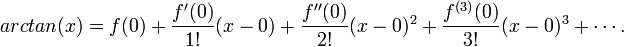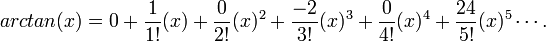MacLaurin series
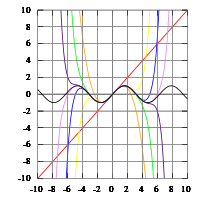
A MacLaurin series is a Taylor series that has a term at (0,0).
Calculus
Notation: let the symbol 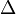 represent change in.
represent change in.
Notation: let the symbol 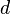 represent an infinitesimal change in.
represent an infinitesimal change in.
Notation: let the symbol 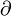 represent an infinitesimal change in one of more than one.
represent an infinitesimal change in one of more than one.
Let
be a function where values of  may be any real number and values resulting in
may be any real number and values resulting in 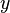 are also any real number.
are also any real number.
-
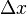 is a small finite change in
is a small finite change in  which when put into the function
which when put into the function  produces a
produces a 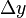 .
.
These small changes can be manipulated with the operations of arithmetic: addition (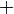 ), subtraction (
), subtraction ( ), multiplication (
), multiplication (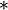 ), and division (
), and division (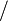 ).
).
Dividing 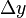 by
by 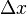 and taking the limit as
and taking the limit as 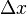 → 0, produces the slope of a line tangent to f(x) at the point x.
→ 0, produces the slope of a line tangent to f(x) at the point x.
For example,
as 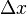 and
and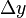 go towards zero,
go towards zero,
This ratio is called the derivative.
Let
then
where z is held constant and
where x is held contstant.
Notation: let the symbol 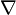 be the gradient, i.e., derivatives for multivariable functions.
be the gradient, i.e., derivatives for multivariable functions.
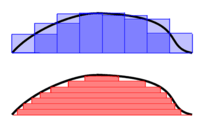
For
the area under the curve shown in the diagram at right is the light purple rectangle plus the dark purple rectangle in the top figure
Any particular individual rectangle for a sum of rectangular areas is
The approximate area under the curve is the sum 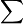 of all the individual (i) areas from i = 0 to as many as the area needed (n):
of all the individual (i) areas from i = 0 to as many as the area needed (n):
Notation: let the symbol 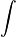 represent the integral.
represent the integral.
This can be within a finite interval [a,b]
when i = 0 the integral is evaluated at 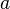 and i = n the integral is evaluated at
and i = n the integral is evaluated at 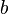 . Or, an indefinite integral (without notation on the integral symbol) as n goes to infinity and i = 0 is the integral evaluated at x = 0.
. Or, an indefinite integral (without notation on the integral symbol) as n goes to infinity and i = 0 is the integral evaluated at x = 0.
Def. a branch of mathematics that deals with the finding and properties ... of infinitesimal differences [or changes] is called a calculus.
"Calculus [focuses] on limits]], functions, derivatives, integrals, and infinite series."[1]
"Although calculus (in the sense of analysis) is usually synonymous with infinitesimal calculus, not all historical formulations have relied on infinitesimals (infinitely small numbers that are nevertheless not zero)."[2]
Series
Taylor Series:
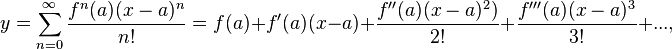
where fn refers to the number (n) of derivatives taken.
A MacLaurin series of a function ƒ(x) for which a derivative may be taken of the function or any of its derivatives at 0 is the power series
which can be written in the more compact sigma, or summation, notation as
where n! denotes the factorial of n and ƒ (n)(0) denotes the nth derivative of ƒ evaluated at the point 0. The derivative of order zero ƒ is defined to be ƒ itself and (x)0 and 0! are both defined to be 1.
MacLaurin series for ex
Taylor series is defined as
The MacLaurin series occurs when t=0
The derivatives are
.
.
.
Development of MacLaurin series for 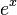
Explicit form can be written as
MacLaurin series for sin(x)
.
.
.
Development of MacLaurin series for 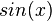
Explicit form can be written as
MacLaurin series for cos(x)
Development of MacLaurin series for 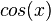
.
.
.
Explicit form can be written as
Euler's formula
Recalling Euler's Formula:
Recall the Taylor Series from above for 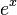 at :
at :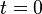 (also called the MacLaurin series)
(also called the MacLaurin series)
By replacing x with 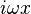 , the Taylor series for
, the Taylor series for 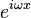 can be found:
can be found:
even powers of n = 2k:
odd powers of n = 2k+1:
For 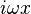 :
:
Using the two previous equations:
Therefore, the first part of the equation is equal to the Taylor series for cosine, and the second part is equal to the Taylor series for sine as follows:
MacLaurin series for 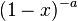
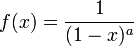
| | |
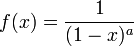 | 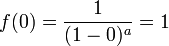 |
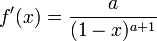 | 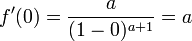 |
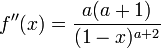 | 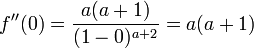 |
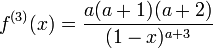 | 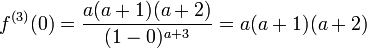 |
| And so on.. | .. |
Rewriting the Maclaurin series expansion,
Substituting the values from the table, we get
Using
We can represent
MacLaurin series for 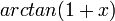
We have the function
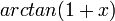
Expand 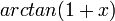
| | |
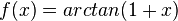 | 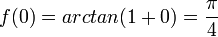 |
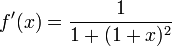 | 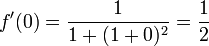 |
![f' '(x) = \frac {-2(x+1)}{\left[1+(1+x)^2\right]^2}](../I/m/c4dec210d8f453825158713858652d07.png) | ![f' '(0) = \frac {-2(0+1)}{\left[1+(1+0)^2\right]^2}= \frac{-1}{2}](../I/m/9dba7c973cf7b5b4f34a9cc2f37d809b.png) |
![f^{(3)}(x) = \frac {2(3x^2+6x+2)}{\left[1+(1+x)^2\right]^3}](../I/m/d07d44afc40c511874cad803795aa2f5.png) | ![f^{(3)}(0) = \frac {2(3(0)^2+6(0)+2)}{\left[1+(1+0)^2\right]^3} = \frac{1}{2}](../I/m/2b527a8a5cc698cf00da3076ebf07f87.png) |
| And so on.. | .. |
Rewriting the Maclaurin series expansion,
Substituting the values from the table, we get
MacLaurin series for 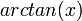
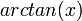
Expanding 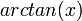 using Maclaurin's series
using Maclaurin's series
| | |
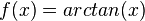 | 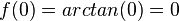 |
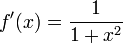 | 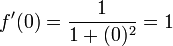 |
![f' '(x) = \frac {-2x}{\left[1+(x)^2\right]^2}](../I/m/a87d929c7391f12195f9a1b2219cf1b0.png) | ![f' '(0) = \frac {-2(0)}{\left[1+(0)^2\right]^2}= 0](../I/m/6b025f5cca00da3b14602f8ca6598b09.png) |
![f^{(3)}(x) = \frac {6x^2-2}{\left[1+(x)^2\right]^3}](../I/m/63da733e93098ceb0dcc0f285df6f1bc.png) | ![f^{(3)}(0) = \frac {6(0)^2-2)}{\left[1+(0)^2\right]^3} = -2](../I/m/0c25adfbbdfebadce1359850608b5b84.png) |
![f^{(4)}(x) = \frac {-24x(x^2-1}{\left[1+(x)^2\right]^4}](../I/m/82beb91be4b6b14b1b670e51712e29ba.png) | ![f^{(4)}(0) = \frac {-24(0)((0)^2-1}{\left[1+(0)^2\right]^4}= 0](../I/m/4570dc9a4f1f135eb1192b954a8b6304.png) |
![f^{(5)}(x) = \frac {24(5x^4-10x^2+1}{\left[1+(x)^2\right]^5}](../I/m/1e9579d4154ae3290c02706371375987.png) | ![f^{(5)}(x) = \frac {24(5(0)^4-10(0)^2+1}{\left[1+(0)^2\right]^5} = 24](../I/m/79ecd310e75ca8612a08ad57ea401b1a.png) |
| And so on.. | .. |
Rewriting the Maclaurin series expansion,
Substituting the values from the table, we get
Engineering
The "performance of a Markov system under different operating strategies [can be estimated] by observing the behavior of the system under the [strategy of having] a Maclaurin series for the performance measures of [the] Markov chains."[3]
Research
Hypothesis:
- Any non-convergent function can be represented by a MacLaurin series.
Control groups

The findings demonstrate a statistically systematic change from the status quo or the control group.
“In the design of experiments, treatments [or special properties or characteristics] are applied to [or observed in] experimental units in the treatment group(s).[4] In comparative experiments, members of the complementary group, the control group, receive either no treatment or a standard treatment.[5]"[6]
Proof of concept
Def. a “short and/or incomplete realization of a certain method or idea to demonstrate its feasibility"[7] is called a proof of concept.
Def. evidence that demonstrates that a concept is possible is called proof of concept.
The proof-of-concept structure consists of
- background,
- procedures,
- findings, and
- interpretation.[8]
See also
- Solution for sin(t)
- Solutions to problem set 2.7
References
- ↑ "Calculus, In: Wikipedia". San Francisco, California: Wikimedia Foundation, Inc. October 13, 2012. Retrieved 2012-10-14.
- ↑ "infinitesimal calculus, In: Wiktionary". San Francisco, California: Wikimedia Foundation, Inc. Setember 19, 2012. Retrieved 2013-01-31.
- ↑ Xi-Ren Cao (1998). "The Maclaurin Series for Performance Functions of Markov Chains". Advances in Applied Probability 30: 676-92. http://www.ece.ust.hk/~eecao/paper/60.pdf. Retrieved 2014-07-23.
- ↑ Klaus Hinkelmann, Oscar Kempthorne (2008). Design and Analysis of Experiments, Volume I: Introduction to Experimental Design (2nd ed.). Wiley. ISBN 978-0-471-72756-9. http://books.google.com/?id=T3wWj2kVYZgC&printsec=frontcover.
- ↑ R. A. Bailey (2008). Design of comparative experiments. Cambridge University Press. ISBN 978-0-521-68357-9. http://www.cambridge.org/uk/catalogue/catalogue.asp?isbn=9780521683579.
- ↑ "Treatment and control groups, In: Wikipedia". San Francisco, California: Wikimedia Foundation, Inc. May 18, 2012. Retrieved 2012-05-31.
- ↑ "proof of concept, In: Wiktionary". San Francisco, California: Wikimedia Foundation, Inc. November 10, 2012. Retrieved 2013-01-13.
- ↑ Ginger Lehrman and Ian B Hogue, Sarah Palmer, Cheryl Jennings, Celsa A Spina, Ann Wiegand, Alan L Landay, Robert W Coombs, Douglas D Richman, John W Mellors, John M Coffin, Ronald J Bosch, David M Margolis (August 13, 2005). "Depletion of latent HIV-1 infection in vivo: a proof-of-concept study". Lancet 366 (9485): 549-55. doi:10.1016/S0140-6736(05)67098-5. http://www.ncbi.nlm.nih.gov/pmc/articles/PMC1894952/. Retrieved 2012-05-09.
External links
- African Journals Online
- Bing Advanced search
- Google Books
- Google scholar Advanced Scholar Search
- International Astronomical Union
- JSTOR
- Lycos search
- NASA/IPAC Extragalactic Database - NED
- NASA's National Space Science Data Center
- NCBI All Databases Search
- Office of Scientific & Technical Information
- Questia - The Online Library of Books and Journals
- SAGE journals online
- The SAO/NASA Astrophysics Data System
- Scirus for scientific information only advanced search
- SDSS Quick Look tool: SkyServer
- SIMBAD Astronomical Database
- SIMBAD Web interface, Harvard alternate
- Spacecraft Query at NASA.
- SpringerLink
- Taylor & Francis Online
- Universal coordinate converter
- Wiley Online Library Advanced Search
- Yahoo Advanced Web Search
![]() This is a research project at http://en.wikiversity.org
This is a research project at http://en.wikiversity.org
| |
Development status: this resource is experimental in nature. |
| |
Educational level: this is a research resource. |
| |
Resource type: this resource contains a lecture or lecture notes. |
| |
Subject classification: this is a mathematics resource . |
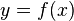
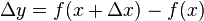
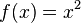
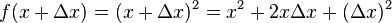
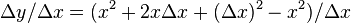
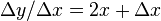
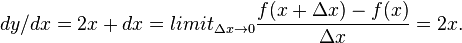
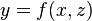
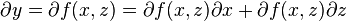
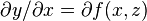
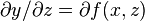
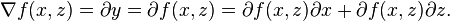
![\Delta x * \Delta y = [f(x + \Delta x) - f(x)] * \Delta x](../I/m/6da4993c799821d9a1d81ba4727956af.png)