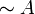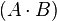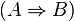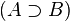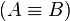Logical Proofs

This page is a learning resource for those people who want to learn how to do logical proofs. Disclaimer: The information provided here is solely from my own experience in a university logic class.

Propositional Translation

For the first part, we are going to learn how to translate natural language into logical expressions. For this we'll use the following tables:

Symbol	Meaning	Translations
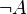
$\lnot A$ $\sim A\,$	Negation	Not A
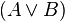$(A \vee B)$	Or	A or B
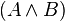
$(A \and B)$ $(A \cdot B)$	And	A and B
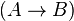
$(A \rightarrow B)$ $(A \Rightarrow B)$ $(A \supset B)$	Implication	If A then B A implies B
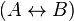
$(A \leftrightarrow B)$ $(A \Leftrightarrow B)$ $(A \equiv B)$	Equivalence	A if and only if B

This article is issued from Wikiversity - version of the Sunday, March 13, 2011. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.