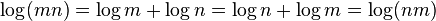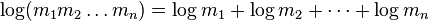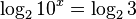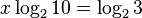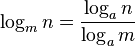Logarithm
Introduction: logarithm as inverse of exponentiation
There are three simple ways equate a with b: using addition, a + cdiff = b, scaling, a * cscaler = b or exponentiation, ac = b. Similarly to the first case, where cdiff is called difference and is computed by subtraction, cdiff = b-a, and the second of multiplication, where factor cscaler = b/a is computed by division (you say that subtraction and division are inverses of the addition and multiplication, correspondingly), the appropriate power c, called exponent, of base a is computed by the logarithm function, c = loga(b). Therefore, the logarithm is a function, inverse of exponentiation.
Actually, because two arguments, the base a and power n, are not commutative in exponentiation an = b, there are two inverse operations. The first one, which computes a, given b and n, is known as n-th root. The logarithm, which computes n, given a and b is the other.
So, basically,
Formal definition
The logarithm is a function of two arguments, a and b, that computes such c
-
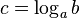
(2 )
that satisfies the equation
-
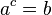
(1 )
The result of the log function is also called logarithm of b with respect to base a or exponent because it is the power that must be applied to the base a to get b.
Properties
The first thing we get by plugging ( ) into ( ):
-
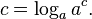
(3.1 )
It basically says that 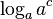 is equivalent to
is equivalent to  . Similar rule is obtained plugging (
) into (
):
. Similar rule is obtained plugging (
) into (
):
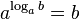
(3.2 )
Because you must raise a into power 1 to get a, you may write
- a¹ = a or
-
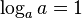
(4.1 )
Similarly, because to get 1 you must raise any number into power 0,
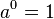 is equivalent to the logarithm property
is equivalent to the logarithm property 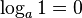
(4.2 )
and, finally,
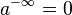 is identical to
is identical to
-
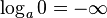
(4.3 )
Note the controversy between ( ) and ( ): log11 = 1 according to the first rule and 0, according to the second.
Log (m*n) = log(m) + log(n)
Without loss of generality, we can define l and m to stand for powers of a,
whereupon, the logarithm of the product is
In short, we arrived at law log of a product equals the sum of the logarithmed operands:
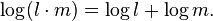
(5 )
The base `a` is omitted because the law holds for any base.
This explains how logarithms replace multiplication with summation. They, further, replace exponentiation with multiplication:
Log (ak) = k log(a)
Decomposing the first term m = m1 * m2 of the equation (5 ) above and using it two times, we can get
You can see that this operation is associative
and commutative
The associativity and commutativity properties are valid for arbitrary number of terms
One important case of having k identical items m1 = m2 = ... = mn = m, gives:
-
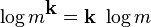
(11 )
If we are not familiar with logarithm of product, the same formula can be proven if we start with a¹=m, whence loga(m)= 1 and, raised to the power, ak=mk gives loga(mk) = k = k * 1 = k loga(m). The same can be demonstrated starting with identity (
), raised to the power k, 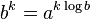 and, applying (
) with mapping
and, applying (
) with mapping 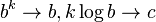 , we get the
, we get the 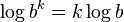 .
.
Similarly, we can prove that factoring the power out of base, has the opposite effect:
-
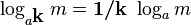
(12 )
Change of bases
Sometimes you have a library that computes logs in some fixed base, say log2, but you need to compute a logarithm of a number, say 3, in some different base, say 10. How do you compute x=log10(3), given log2 function? You need to compute such x that 10x = 3. Apply log2 to both left and right to get
Apply the last property of (11 )
and divide both sides by 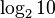 and get
and get
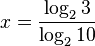 .
.
Generally,
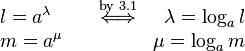
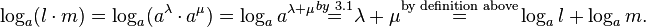
![\log [(m_1 m_2) n] = \log (m_1 m_2) + \log n = \log m_1 + \log m_2 + \log n](../I/m/76f9ca955773f697eb61876ab965f8bf.png)
![\log [m_1 (m_2 n)] = \log m_1 + (\log m_2 + \log n)](../I/m/5348882ca90085a717325aeb94953816.png)