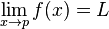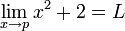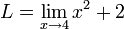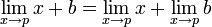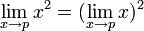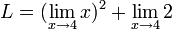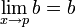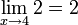Limits

Limits of Functions

Basics

What are limits?

Limits are a way to calculate the value that a function approaches. For instance, we could calculate the value of the function f(x) as x approaches 2. Just as easily we can calculate the value of f(x) as x approaches 20, -2, π, 0, or even ∞.

Why would anyone need limits?

There are a number of reasons that someone might want to use limits:

1. To find the values of functions with asymptotes or missing points

2. To calculate the slope of a point in calculus

3. To prove derivatives in calculus

Notation

The notation of a limit function is fairly simple:

\lim_{x \to p}f(x) = L

This says limit (lim) of f(x) as x approaches p is L.

Usually f(x) is substituted with the contents of the function like so:

\lim_{x \to p}x^2+2 = L

Sample Problem Set #1

Let's say we have the function 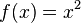$f(x)=x^2$ . If we want to find the limit as x approaches 4, then:

L = \lim_{x \to 4}x^2+2

Using two properties of limits:

\lim_{x \to p}x+b = \lim_{x \to p}x + \lim_{x \to p}b

and

\lim_{x \to p}x^2 = (\lim_{x \to p}x)^2

Our problem becomes:

L = (\lim_{x \to 4}x)^2 + \lim_{x \to 4}2

If we think about the graph of y=b, then we know that the y value never changes. Which means that at any point on that line, we can expect y to be equal to b. So, for any number b:

\lim_{x \to p}b = b

For us, this means that:

\lim_{x \to 4}2 = 2

This article is issued from Wikiversity - version of the Thursday, February 11, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.