Light in moving media

Requisites

Relativistic addition of velocities

Refractive index

Problem

Light moves through a slowly moving medium with refractive index n. That medium moves with a speed v in parallel with the direction of light. What speed will be measured for that light by a rest observer?

Solution

If we have a medium with refractive index n, the speed of light relative to that medium is c/n.

Using relativistic addition of velocities, we get for the rest observer:

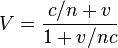
V=\frac{c/n+v}{1+v/nc}

But as 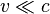$v \ll c$ , we can expand that expression in terms of $v/c$ :

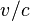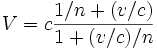
$V=c \frac{1/n+(v/c)}{1+(v/c)/n}$

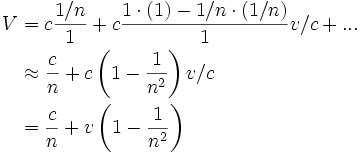
$\begin{align} V & =c \frac{1/n}{1} +c \frac{1 \cdot(1)-1/n \cdot(1/n)}{1} v/c + ... \\ & \approx \frac{c}{n} +c \left (1 - \frac{1}{n^2} \right ) v/c \\ & = \frac{c}{n} +v \left (1 - \frac{1}{n^2} \right ) \\ \end{align}$

The factor 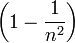$\left (1 - \frac{1}{n^2} \right )$ was known as the Fresnel drag coefficient. It is easily measured with interference experiments.

Generalization

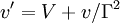
v'=V+v/\Gamma^2

This article is issued from Wikiversity - version of the Monday, April 04, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.