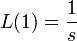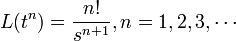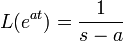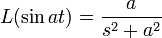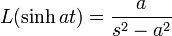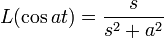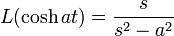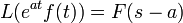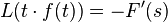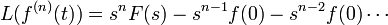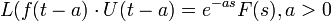Laplace transforms
| | Educational level: this is a tertiary (university) resource. |
| | Resource type: this resource is a lesson. |
| | Subject classification: this is a mathematics resource . |
| | Completion status: this resource is ~25% complete. |
School:Mathematics > Topic:Differential_Equations > Ordinary Differential Equations > Laplace Transforms
Definition
For some problems, the Laplace transform can convert the problem into a more solvable form. The Laplace transform equation is defined as 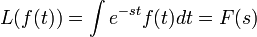 . There are many properties of the Laplace transform that make it desirable to work with, such as linearity, or in other words,
. There are many properties of the Laplace transform that make it desirable to work with, such as linearity, or in other words, 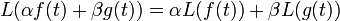 .
.
Solution
To illustrate how to solve a differential equation using the Laplace transform, let's take the following equation: 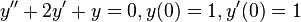 . The Laplace transform usually is suited for equations with initial conditions.
. The Laplace transform usually is suited for equations with initial conditions.
- Take the Laplace transform of both sides (
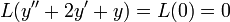 ).
). - Use the associative property to split the left side into terms (
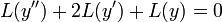 ).
). - Use the theorem
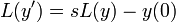 , and by extension,
, and by extension, 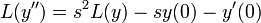 to modify the terms into scalars and multiples of
to modify the terms into scalars and multiples of 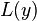 (
(![s^2L(y)-sy(0)-y'(0)+2 \left [ sL(y)-y(0) \right ] +L(y)=0](../I/m/ba374df25c720e22c0be1160a04ef094.png) ).
). - Solve for the Laplacian (
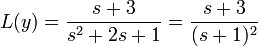 ).
). - Take the inverse Laplace transform of both sides to get the solution, solving by method of partial fractions as needed:
(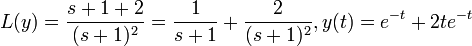 ).
). - For reference, here are some basic Laplace transforms:
- For reference, here are some theorems for the Laplace transforms:
This article is issued from Wikiversity - version of the Saturday, July 09, 2011. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.