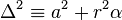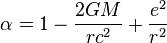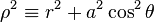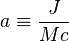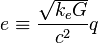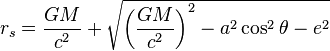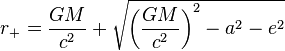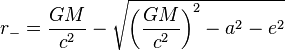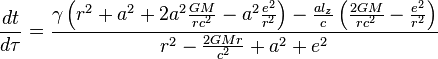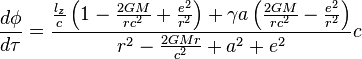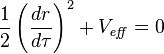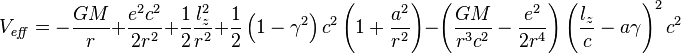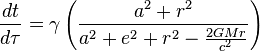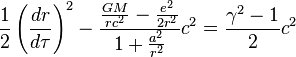Kerr–Newman metric

Resource type: this resource contains a lecture or lecture notes.

Search for Kerr–Newman metric on Wikipedia.

Search for Kerr–Newman metric on the following projects:

Educational level: this is a tertiary (university) resource.

Subject classification: this is a physics resource .

The spacetime metric is, in Boyer-Lindquist coordinates,

ds^2 = \frac{\Delta^2}{\rho^2} (dct - a\, \sin^2\theta \, d\phi)^2 - \frac{\sin^2\theta}{\rho^2} [ (r^2 + a^2) d\phi - a\, dct]^2 - \frac{\rho^2}{\Delta^2} dr^2 - \rho^2 d\theta^2

where

\Delta^2 \equiv a^2 +r^2\alpha

\alpha = 1 - \frac{2GM}{rc^2} + \frac{e^2}{r^2}

\rho ^2 \equiv r^2 + a^2\cos^2\theta

a \equiv \frac{J}{Mc}

e \equiv \frac{\sqrt{k_{e}G}}{c^2}q

This represents the exact solution to General relativity/Einstein equations for the stress-energy tensor for an electromagnetic field from a charged rotating black hole. In the case that the charge 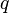$q$ is zero it becomes an exact vacuum solution to Einstein's field equations and is called just "the Kerr solution".

Mathematical Surfaces

There are three important mathematical surfaces for this line element, the static limit and the inner and outer event horizons. The static limit is the outermost place something can be outside the outer horizon with a zero angular velocity. It is

r_s = \frac{GM}{c^2}+\sqrt{\left(\frac{GM}{c^2}\right)^2 - a^2 \cos^2 \theta -e^2}

The event horizons are coordinate singularities in the metric where 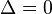$\Delta = 0$ .

The outer event horizon is at

r_{+} = \frac{GM}{c^2}+\sqrt{\left(\frac{GM}{c^2}\right)^2 - a^2 -e^2}

and the inner horizon is at

r_{-} = \frac{GM}{c^2}-\sqrt{\left(\frac{GM}{c^2}\right)^2 - a^2 -e^2}

An external observer can never see an event at which something crosses into the outer horizon. A remote observer reckoning with these coordinates will reckon that it takes an infinite time for something infalling to reach the outer horizon even though it takes a finite proper time till the event according to what fell in.

Kerr-Newman Equatorial Geodesic Motion

The exact equations of equatorial geodesic motion for a neutral test mass in a charged and rotating black hole's spacetime are

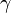\frac{dt}{d\tau}=\frac{\gamma \left(r^2 +a^2 +2a^2 \frac{GM}{rc^2}-a^2 \frac{e^2}{r^2}\right)-\frac{al_{z}}{c} \left(\frac{2GM}{rc^2}-\frac{e^2}{r^2}\right)}{r^2 -\frac{2GMr}{c^2} + a^2 +e^2}

\frac{d\phi}{d\tau}=\frac{\frac{l_z}{c} \left(1-\frac{2GM}{rc^2}+\frac{e^2}{r^2}\right)+\gamma a\left(\frac{2GM}{rc^2 }-\frac{e^2}{r^2}\right)}{r^2 -\frac{2GMr}{c^2}+ a^2 +e^2}c

\frac{1}{2}\left(\frac{dr}{d\tau}\right)^2 +V_{\it eff} =0

V_{\it eff} = -\frac{GM}{r}+\frac{e^2 c^2 }{2r^2}+\frac{1}{2}\frac{l_z ^2}{r^2} +\frac{1}{2}\left(1-\gamma ^2\right)c^2 \left(1+\frac{a^2}{r^2}\right)-\left(\frac{GM}{r^3 c^2 }-\frac{e^2}{2r^4}\right)\left(\frac{l_z}{c} -a\gamma \right)^2 c^2

where $\gamma$ is the conserved energy parameter, the energy per 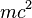$mc^2$ of the test mass and 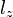$l_z$ is the conserved angular momentum per mass 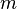$m$ for the test mass.

Kerr-Newman Polar Geodesic Motion

The exact equations of polar geodesic motion for a neutral test mass in a charged and rotating black hole's spacetime are

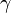\frac{dt}{d\tau }=\gamma \left(\frac{a^2 +r^2}{a^2 +e^2 +r^2 -\frac{2GMr}{c^2}}\right)

\frac{1}{2}\left(\frac{dr}{d\tau}\right)^2 - \frac{\frac{GM}{rc^2}-\frac{e^2}{2r^2}}{1+\frac{a^2}{r^2}}c^2 = \frac{\gamma ^2 -1}{2}c^2

where $\gamma$ is the conserved energy parameter, the energy per 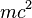$mc^2$ of the test mass.

Wormhole Structure

Penrose diagram for coordinate extension of a charged or rotating black hole

Above we see a Penrose diagram representing a coordinate extension (1) for a charged or rotating black hole. The same way as mapping Schwarzschild coordinates onto Kruskal-Szekeres coordinate reveals two seperate external regions for the Schwarzschild black hole, such a mapping done for a charged or rotating hole reveals an even more multiply connected region for charged and rotating black holes. Lets say region I represents our external region outside a charged black hole. In the same way that the other external region is inaccessible as the wormhole connection is not transversible, external region II is also not accessible from region I. The difference is that there are other external regions VII and VIII which are ideed accessible from region I by transversible paths at least one way. One should expect this as the radial movement case of geodesic motion for a neutral test particle written above leads back out of the hole without intersecting the physical singularity at 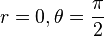$r=0, \theta = \frac{\pi }{2}$ .

References

(1)Black Holes-Parts 4&5 pp 26-42

Relativity