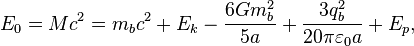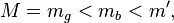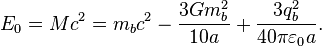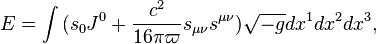Invariant energy
Invariant energy of an arbitrary physical system is a positive quantity, which consists of all types of energies of the system, and is equal to the relativistic energy, measured by the observer who is fixed relative to the center of mass of the system. The invariant energy usually includes the rest energy of the matter; the potential energy of the proper electromagnetic and gravitational fields associated with the system; the internal energy of the system’s particles; the energy of the system in external fields; the energy of emission interacting with the system. The invariant energy 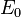 of a particle equals to its rest energy and due to the principle of mass–energy equivalence is associated with the invariant mass
of a particle equals to its rest energy and due to the principle of mass–energy equivalence is associated with the invariant mass 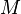 of the particle by the equation:
of the particle by the equation:
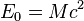 ,
,
where  is the speed of light.
is the speed of light.
The order of calculating the invariant energy through various types of energy of the system is determined by the principle of energies summation.
Relationship with other physical variables
One particle
In the special relativity, the invariant energy of the particle can be calculated either through its relativistic energy 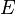 and momentum
and momentum 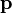 , or through the relativistic energy and the velocity
, or through the relativistic energy and the velocity 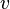 :
:
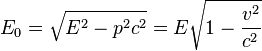 .
.
The relation 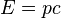 holds for the photon, so that the invariant energy of the photon is zero.
holds for the photon, so that the invariant energy of the photon is zero.
In four-dimensional formalism in Minkowski space the energy 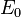 can be calculated through the 4-momentum
can be calculated through the 4-momentum 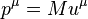 of the particle:
of the particle:
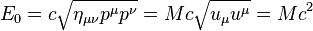 ,
,
where 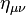 is the metric tensor of the Minkowski space,
is the metric tensor of the Minkowski space, 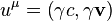 is 4-velocity,
is 4-velocity, 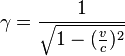 is the Lorentz factor.
is the Lorentz factor.
As a result, 4-momentum can be represented using the invariant energy: [1]
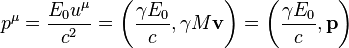 ,
,
where 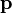 is the 3-vector of relativistic momentum.
is the 3-vector of relativistic momentum.
In the curved spacetime with the metric tensor 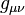 the invariant energy of the particle is found as follows:
the invariant energy of the particle is found as follows:
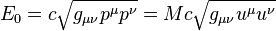 .
.
If we take into account the definition of 4-velocity: 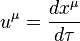 , where
, where 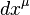 is 4-displacement vector,
is 4-displacement vector, 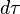 is the differential of the proper time; and the definition of the spacetime interval:
is the differential of the proper time; and the definition of the spacetime interval: 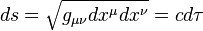 , then again we obtain the equality:
, then again we obtain the equality: 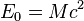 .
.
The system of particles
In elementary particle physics the interaction of several particles, their coalescence and decay with formation of new particles are often considered. Conservation of the sum of 4-momenta of free particles before and after the reaction leads to the conservation laws of energy and momentum of the system of particles under consideration. The invariant energy 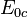 of the system of particles is calculated as their total relativistic energy in the reference frame in which the center of mass of the particle system is stationary. In this case
of the system of particles is calculated as their total relativistic energy in the reference frame in which the center of mass of the particle system is stationary. In this case 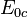 can differ from the sum of invariant energies of the particles of the system, since the contribution into
can differ from the sum of invariant energies of the particles of the system, since the contribution into 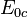 is made not only by the rest energies of the particles, but also by the kinetic energies of the particles and their potential energy. [2] If we observe the particles before or after the interaction at large distances from each other, when their mutual potential energy can be neglected, the invariant energy of the system is defined as:
is made not only by the rest energies of the particles, but also by the kinetic energies of the particles and their potential energy. [2] If we observe the particles before or after the interaction at large distances from each other, when their mutual potential energy can be neglected, the invariant energy of the system is defined as:
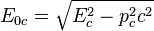 ,
,
where 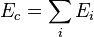 is the sum of relativistic energies of the system’s particles,
is the sum of relativistic energies of the system’s particles, 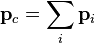 is the vector sum of the particles’ momenta.
is the vector sum of the particles’ momenta.
The massive body
General relativity
In determining the invariant energy of a massive body in general relativity (GR) there is a problem with the contribution of the gravitational field energy, [3] since the stress-energy tensor of gravitational field is not clearly defined, and stress-energy-momentum pseudotensor is used instead. In case of asymptotically flat spacetime at infinity for the estimation of the invariant energy the ADM formalism for the mass-energy of the body can be applied. [4] For the stationary spacetime metric the Komar mass and energy are determined. [5] There are other approaches to determination of the mass-energy, such as Bondi energy, [6] and Hawking energy.
In the weak-field approximation the invariant energy of a stationary body in GR is estimated as follows: [7]
where the mass 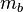 and charge
and charge 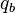 of body are obtained by integrating the corresponding density by volume,
of body are obtained by integrating the corresponding density by volume, 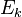 is the energy of motion of particles inside the body,
is the energy of motion of particles inside the body, 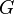 is the gravitational constant,
is the gravitational constant, 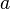 is the radius of the body,
is the radius of the body, 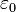 is the vacuum permittivity,
is the vacuum permittivity, 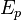 is the pressure energy.
is the pressure energy.
For the masses, the relation is:
where the mass of the system 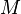 is equal to the gravitational mass
is equal to the gravitational mass 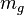 , the mass
, the mass 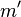 denotes the total mass of the particles that compose the body.
denotes the total mass of the particles that compose the body.
Covariant theory of gravitation
In covariant theory of gravitation (CTG) in the calculation of the invariant energy the energy partition into 2 main parts is used – for the components of the energy fields themselves and for components associated with the energy of the particles in these fields. Calculation shows that the sum of the components of the energy of acceleration field, pressure field, gravitational and electromagnetic fields, for the spherical shape of the body is zero. [8] As a result there is only a sum of the energies of the particles in the four fields:
The ratio of the masses is as follows:
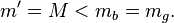
In CTG the system mass 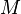 equals the total mass of particles
equals the total mass of particles 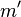 at infinity, the mass
at infinity, the mass 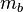 equals the gravitational mass
equals the gravitational mass 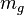 and excess
and excess 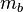 over
over 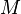 is due to the fact that particles move inside the body and are under pressure in the gravitational and electromagnetic fields.
is due to the fact that particles move inside the body and are under pressure in the gravitational and electromagnetic fields.
In Lorentz-invariant theory of gravitation (LITG), in which CTG is transformed in the weak-field approximation and at a constant velocity of motion, for the invariant energy the following formula holds:
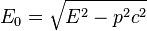 ,
,
where 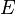 is the relativistic energy of a moving body taking into account the contribution of the gravitational and electromagnetic field energy,
is the relativistic energy of a moving body taking into account the contribution of the gravitational and electromagnetic field energy, 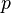 is the total momentum of the system.
is the total momentum of the system.
These formulas remain valid at the atomic level, with the difference that the usual gravity replaced by strong gravitation. In the covariant theory of gravitation based on the principle of least action is shown that the gravitational mass 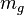 of the system increases due to the contribution of mass-energy of the gravitational field, and decreases due to the contribution of the electromagnetic mass-energy. This is the consequence of the fact that in LITG and in CTG the gravitational stress-energy tensor is accurately determined, which is one of the sources for the determining the metric, energy and the equations of motion of matter and field. The acceleration stress-energy tensor, dissipation stress-energy tensor and pressure stress-energy tensor are also identified in covariant form.
of the system increases due to the contribution of mass-energy of the gravitational field, and decreases due to the contribution of the electromagnetic mass-energy. This is the consequence of the fact that in LITG and in CTG the gravitational stress-energy tensor is accurately determined, which is one of the sources for the determining the metric, energy and the equations of motion of matter and field. The acceleration stress-energy tensor, dissipation stress-energy tensor and pressure stress-energy tensor are also identified in covariant form.
Vector fields such as the gravitational and electromagnetic fields, the acceleration field, the pressure field, the dissipation field, the fields of strong and weak interactions are components of general field. This leads to the fact that the invariant energy of the system of particles and fields can be calculated as the volumetric integral in the center-of-momentum frame: [9]
where 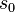 and
and 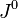 denote the time components of the 4-potential
denote the time components of the 4-potential 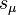 of general field and the mass 4-current
of general field and the mass 4-current 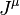 , respectively,
, respectively, 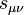 is the tensor of the general field.
is the tensor of the general field.
See also
- Invariant mass
- Principle of energies summation
- Field mass-energy limit
- General field
- Dissipation field
- Acceleration field
- Pressure field
References
- ↑ McGlinn, William D. (2004), Introduction to relativity, JHU Press, ISBN 0-8018-7047-X, http://books.google.com/books?id=PoDYLk6Ugd8C, Extract of page 43
- ↑ Landau L.D., Lifshitz E.M. (1975). The Classical Theory of Fields. Vol. 2 (4th ed.). Butterworth-Heinemann. ISBN 978-0-750-62768-9.
- ↑ Misner, Charles W.; Kip. S. Thorne & John A. Wheeler (1973), Gravitation, W. H. Freeman, ISBN 0-7167-0344-0
- ↑ Arnowitt, Richard; Stanley Deser & Charles W. Misner (1962), "The dynamics of general relativity", in Witten, L., Gravitation: An Introduction to Current Research, Wiley, pp. 227-265.
- ↑ Komar, Arthur (1959). "Covariant Conservation Laws in General Relativity". Phys. Rev. 113 (3): 934–936. Bibcode 1959PhRv..113..934K. doi:10.1103/PhysRev.113.934
- ↑ Bondi H, van de Burg M G J, and Metzner A W K, Proc. R. Soc. London Ser. A 269:21-52 Gravitational waves in General Relativity. VII. Waves from axi-symmetric isolated systems (1962).
- ↑ V. A. Fock, The Theory of Space, Time and Gravitation (Pergamon Press, London, 1959).
- ↑ Fedosin S.G. Relativistic Energy and Mass in the Weak Field Limit. Jordan Journal of Physics. Vol. 8 (No. 1), pp. 1-16, (2015).
- ↑ Fedosin S.G. The Concept of the General Force Vector Field. OALib Journal, Vol. 3, P. 1-15 (2016), e2459. http://dx.doi.org/10.4236/oalib.1102459.