Introduction to group theory/Right cancellation
< Introduction to group theory- Proof
Let 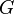 be a group and let
be a group and let 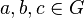 such that
such that 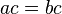 .
Since
.
Since 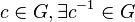 such that
such that 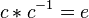 .
Multiplying
.
Multiplying 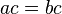 on each side by
on each side by 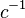 we obtain.
we obtain.
 .
Applying the definition of inverses (
.
Applying the definition of inverses (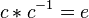 ) we get
) we get
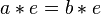 Applying the definition of identity we get
Applying the definition of identity we get
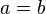
- Q.E.D.
This article is issued from Wikiversity - version of the Wednesday, July 17, 2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.