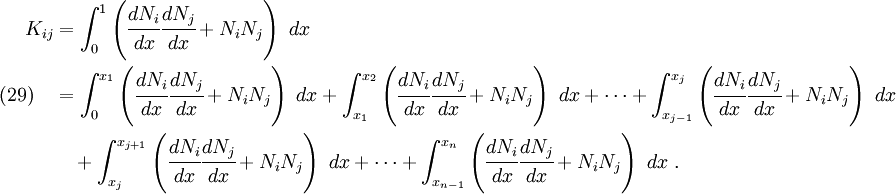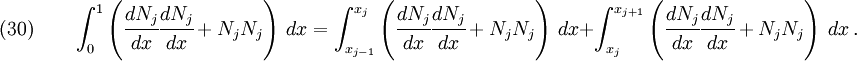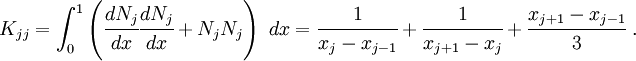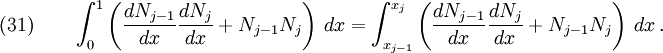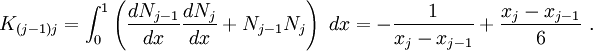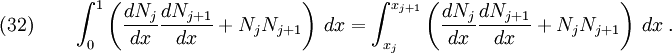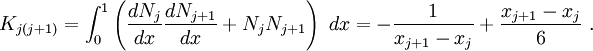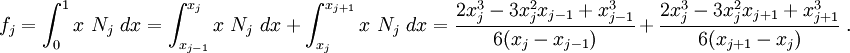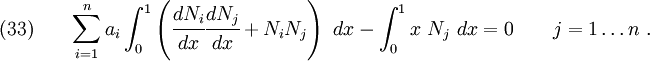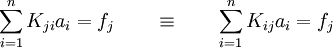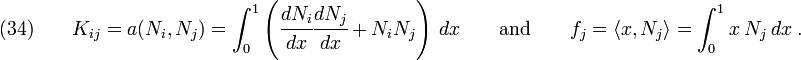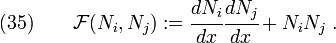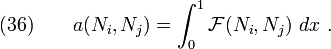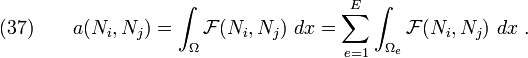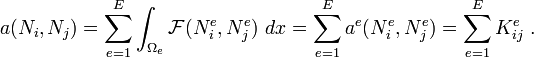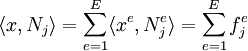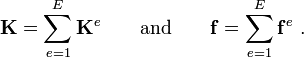Introduction to finite elements/Model finite element approximation
< Introduction to finite elementsFinite Element Formulation for Problem 2.
The domain for this problem is 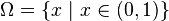 and the boundary consists of two points
and the boundary consists of two points 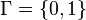 . Let us use
. Let us use  nodes in the domain so that they divide the domain into
nodes in the domain so that they divide the domain into 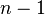 nonoverlapping, two-noded elements.
nonoverlapping, two-noded elements.
Consider the term 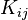 in equation (22). The integral can be written as a sum of integrals over each element as
in equation (22). The integral can be written as a sum of integrals over each element as
In this equation, 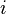 and
and 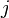 are node numbers. Therefore there are
are node numbers. Therefore there are 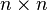 possible values of
possible values of 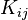 .
.
Assume that node 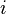 = 2 and node
= 2 and node 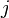 = 4. Then
= 4. Then 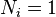 at node 2 and zero at all the other nodes. Similarly,
at node 2 and zero at all the other nodes. Similarly, 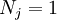 at node 4 and zero at all other nodes. Also,
at node 4 and zero at all other nodes. Also, 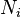 is non-zero only between nodes 1, 2, and 3 while
is non-zero only between nodes 1, 2, and 3 while 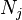 is nonzero only between nodes 3, 4, and 5. Since the domains of
is nonzero only between nodes 3, 4, and 5. Since the domains of 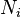 and
and 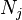 do not overlap in this case, all the integrals must be zero.
do not overlap in this case, all the integrals must be zero.
In general, if 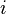 and
and 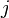 are separated by more than one node, at least one of the basis functions has a zero value within each integral. The same holds for the derivatives of the basis functions. Therefore
are separated by more than one node, at least one of the basis functions has a zero value within each integral. The same holds for the derivatives of the basis functions. Therefore 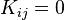 if
if 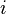 and
and 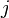 are separated by more than one node.
are separated by more than one node.
Therefore, there are three non-trivial cases that need to be looked at
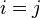 .
.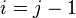 .
.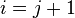 .
.
For the first case, set 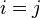 in equation (29).
That means
in equation (29).
That means
After substituting the values of the basis functions (25) and their derivatives (26) into equation (30) and integrating, we get
For the second case, set 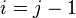 in equation (29). In this case, the only non-zero integrals in equation (29) are the ones between
in equation (29). In this case, the only non-zero integrals in equation (29) are the ones between 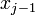 and
and 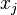 . Hence
. Hence
After substituting the basis functions and their derivatives into equation (31) and integrating, we get
For the third case, set 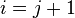 in equation (29). In this case, the only non-zero integrals in equation (29) are the ones between
in equation (29). In this case, the only non-zero integrals in equation (29) are the ones between 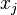 and
and 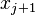 . Hence
. Hence
After substituting the basis functions and their derivatives into equation (\ref{eq:Integralij+1}) and integrating, we get
The same process can be followed for the integral
Now that we know the components 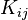 and
and 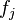 , we can solve the system of equations (23) for the unknowns
, we can solve the system of equations (23) for the unknowns 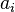 . This gives us our finite element solution for Problem 2.
. This gives us our finite element solution for Problem 2.
Assembly process.
In the above we did not go through the assembly process that you are familiar with from introductory finite elements. We can simplify things if we use just compute the integrals over each element and assemble them to get the final 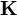 and
and 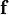 matrices.
matrices.
To see how the assembly process works, let us recall equation (21)
We can rewrite this equation as
where
Let us define
Then the first of the equations in (34) can be written as
From equation (29) we can see that the integral over the entire domain  can be written as a sum of integrals over the elements
can be written as a sum of integrals over the elements 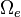 . Therefore, we can write equation (36) as
. Therefore, we can write equation (36) as
Let 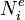 be the local basis functions in an element. Then equation (37) can be written as
be the local basis functions in an element. Then equation (37) can be written as
Similarly, the second equation in (34) can be written as
where 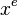 indicates that the integral is over the element.
indicates that the integral is over the element.
Therefore, the matrix 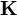 and the vector
and the vector 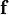 can be expressed as a sum over the elements in the form
can be expressed as a sum over the elements in the form
This is the familiar assembly process. From this process it is clear that if we can find the weak form for one element, then the finite element system of equations for any combination of such elements can be computed by assembly.