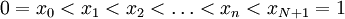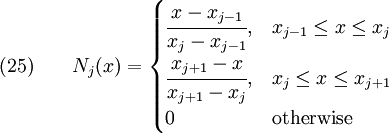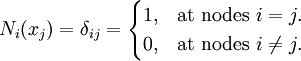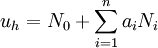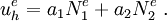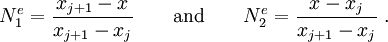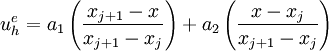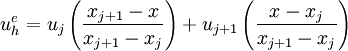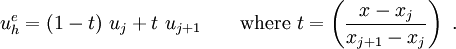Introduction to finite elements/Finite element basis functions
< Introduction to finite elementsFinite Element Basis Functions
The Finite Element Method provides a general and systematic technique for constructing basis functions for Galerkin's approximation of boundary value problems.
The idea of finite elements is to choose  piecewise over subregions of the domain called finite elements. Such functions can be very simple, for example, polynomials of low degree. We measure the size of each subregion with a parameter
piecewise over subregions of the domain called finite elements. Such functions can be very simple, for example, polynomials of low degree. We measure the size of each subregion with a parameter  . As
. As  decreases more elements are introduced and more basis functions are needed. The square integrability condition implies that jumps in the value of the function are not allowed at the nodes.
decreases more elements are introduced and more basis functions are needed. The square integrability condition implies that jumps in the value of the function are not allowed at the nodes.
The simplest basis functions are piecewise linear functions and the corresponding elements are line segments in 1D, triangles and quadrilaterals in 2D, and tetrahedra, prisms and hexahedra in 3D.
These basis functions have to be chosen from the space 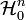 . Let
. Let 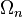 be the space of piecewise linear functions. It can be shown that
be the space of piecewise linear functions. It can be shown that 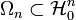 .
.
Let
be a partition of ![[0,1]](../I/m/ccfcd347d0bf65dc77afe01a3306a96b.png) into subintervals
into subintervals 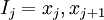 of length
of length
Let 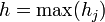 be a measure of overall fineness of the grid. Let us choose as basis functions the set of triangular functions shown in Figure 1.
be a measure of overall fineness of the grid. Let us choose as basis functions the set of triangular functions shown in Figure 1.
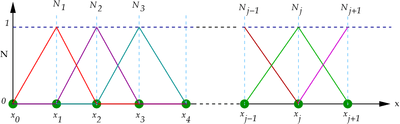 Figure 1. Finite element basis functions. |
In algebraic form, these basis functions are defined as
Note that the shape functions also satisfy the following,
The first derivatives of the basis functions are
So there are discontinuities in the first derivatives at 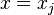 as you can see in Figure 2.
as you can see in Figure 2.
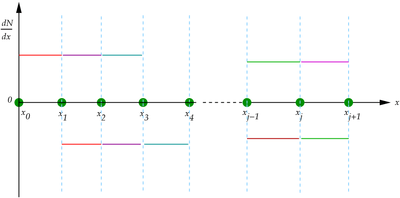 Figure 2. Derivatives of finite element basis functions. |
The Galerkin trial solution is
where  is the number of nodes in an element. If we have two nodes per element as shown in Figure 2, then within each element we have
is the number of nodes in an element. If we have two nodes per element as shown in Figure 2, then within each element we have
The basis functions 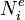 are the element (or local) basis functions and are to be distinguished from the global basis functions centered around nodes.
are the element (or local) basis functions and are to be distinguished from the global basis functions centered around nodes.
If you look at the element that joins node 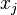 to node
to node 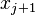 you will see that there are two functions
you will see that there are two functions 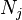 and
and 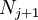 that describe this element. The local basis functions for the element are therefore
that describe this element. The local basis functions for the element are therefore
Hence we can write
If we force the solution 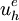 to be equal to
to be equal to 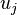 at
at 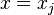 and
and 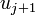 at
at 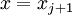 , we get
, we get 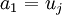 and
and 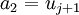 .
.
Therefore, the solution is approximated by the piecewise linear function,
We could also write
This a parametric representation of a line and shows very clearly that 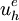 is a linear approximation. Figure 3 shows a schematic of a FE solution using linear shape functions.
is a linear approximation. Figure 3 shows a schematic of a FE solution using linear shape functions.
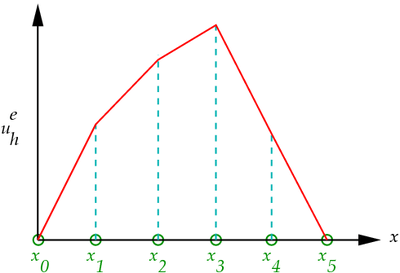 Figure 3. Schematic of a finite element solution computed using linear shape functions. |