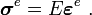Introduction to finite elements/Axial bar finite element solution
< Introduction to finite elementsAxially loaded bar: The Finite Element Solution
The finite element method is a type of Galerkin method that has the following advantages:
- The functions
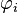 are found in a systematic manner.
are found in a systematic manner. - The functions
 are chosen such that they can be used for arbitrary domains.
are chosen such that they can be used for arbitrary domains. - The functions
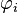 are piecewise polynomials.
are piecewise polynomials. - The functions
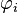 are non-zero only on a small part of the domain.
are non-zero only on a small part of the domain.
As a result, computations can be done in a modular manner that is suitable for computer implementation.
Discretization
The first step in the finite element approach is to divide the domain into elements and nodes, i.e., to create the finite element mesh.
Let us consider a simple situation and divide the rod into 3 elements and 4 nodes as shown in Figure 6.
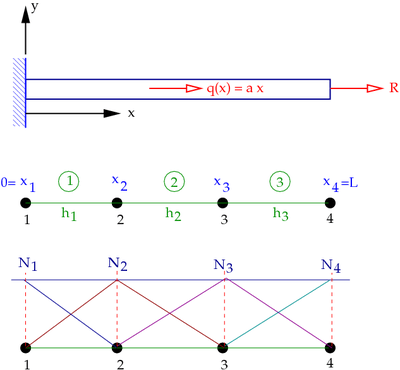 Figure 6. Finite element mesh and basis functions for the bar. |
Shape functions
The functions 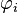 have special characteristics in finite element methods and are generally written as
have special characteristics in finite element methods and are generally written as 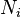 and are called basis functions, shape functions, or interpolation functions.
and are called basis functions, shape functions, or interpolation functions.
Therefore, we may write
The finite element basis functions are chosen such that they have the following properties:
- The functions
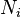 are bounded and continuous.
are bounded and continuous. - If there are
 nodes, then there are
nodes, then there are  basis functions - one for each node. There are four basis functions for the mesh shown in Figure 6.
basis functions - one for each node. There are four basis functions for the mesh shown in Figure 6. - Each function
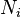 is nonzero only on elements connected to node
is nonzero only on elements connected to node 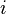 .
. 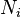 is 1 at node
is 1 at node 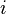 and zero at all other nodes.
and zero at all other nodes.
Stiffness matrix
Let us compute the values of 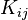 for the three element mesh. We have
for the three element mesh. We have
The components of 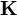 are
are
The matrix 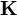 is symmetric, so we don't need to explicitly compute the other terms.
is symmetric, so we don't need to explicitly compute the other terms.
From Figure 6, we see that 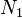 is zero in elements 2 and 3,
is zero in elements 2 and 3, 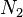 is zero in element 3,
is zero in element 3, 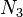 is zero in element 1, and
is zero in element 1, and 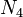 is zero in elements 1 and 2. The same holds for
is zero in elements 1 and 2. The same holds for 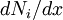 .
.
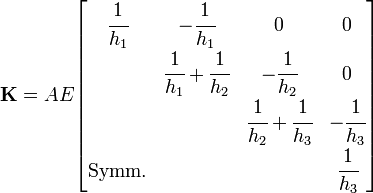
Therefore, the coefficients of the 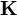 matrix become
matrix become
We can simplify our calculation further by letting 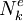 be the shape functions over an element
be the shape functions over an element  . For example, the shape functions over element
. For example, the shape functions over element 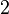 are
are 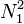 and
and 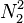 where the local nodes
where the local nodes 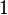 and
and 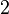 correspond to global nodes
correspond to global nodes 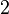 and
and 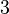 , respectively. Then we can write,
, respectively. Then we can write,
Let 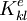 be the part of the value of
be the part of the value of 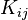 that is contributed by element
that is contributed by element  . The indices
. The indices 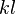 are local and the indices
are local and the indices 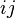 are global. Then,
are global. Then,
We can therefore see that if we compute the stiffness matrices over
each element and assemble them in an appropriate manner, we can get the
global stiffness matrix 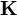 .
.
Stiffness matrix for two-noded elements
For our problem, if we consider an element  with two nodes, the local hat shape functions have the form
with two nodes, the local hat shape functions have the form
where 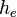 is the length of the element.
is the length of the element.
Then, the components of the element stiffness matrix are
In matrix form,
The components of the global stiffness matrix are
In matrix form,
Load vector
Similarly, for the load vector 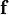 , we have
, we have
The components of the load vector are
Once again, since 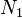 is zero in elements 2 and 3,
is zero in elements 2 and 3, 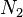 is zero in element 3,
is zero in element 3, 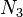 is zero in element 1, and
is zero in element 1, and 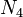 is zero in elements 1 and 2, we have
is zero in elements 1 and 2, we have
Now, the boundary 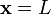 is at node 4 which is attached to element 3. The only non-zero shape function at this node is
is at node 4 which is attached to element 3. The only non-zero shape function at this node is 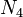 . Therefore, we have
. Therefore, we have
In terms of element shape functions, the above equations can be written as
The above shows that the global load vector can also be assembled from the element load vectors if we use finite element shape functions.
Load vector for two-noded elements
Using the linear shape functions discussed earlier and replacing 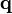 with
with 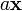 , the components of the element load vector
, the components of the element load vector 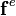 are
are
In matrix form, the element load vector is written
Therefore, the components of the global load vector are
Displacement trial function
Recall that we assumed that the displacement can be written as
If we use finite element shape functions, we can write the above as
where  is the total number of nodes in the domain. Also, recall that the value of
is the total number of nodes in the domain. Also, recall that the value of 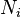 is 1 at node
is 1 at node 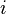 and zero elsewhere. Therefore, we have
and zero elsewhere. Therefore, we have
Therefore, the trial function can be written as
where 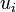 are the nodal displacements.
are the nodal displacements.
Finite element system of equations
If all the elements are assumed to be of the same length 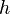 , the finite element system of equations (
, the finite element system of equations (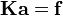 ) can then be written as
) can then be written as
Essential boundary conditions
To solve this system of equations we have to apply the essential boundary condition 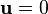 at
at 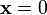 . This is equivalent to setting
. This is equivalent to setting 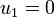 . The reduced system of equations is
. The reduced system of equations is
This system of equations can be solved for 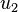 ,
, 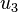 , and
, and 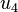 . Let us do that.
. Let us do that.
Assume that 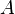 ,
,  ,
, 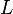 ,
, 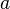 , and
, and 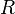 are all equal to 1. Then
are all equal to 1. Then 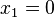 ,
, 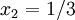 ,
, 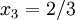 ,
, 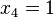 , and
, and 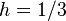 . The system of equations becomes
. The system of equations becomes
Computing element strains and stresses
From the above, it is clear that the displacement field within an element  is given by
is given by
Therefore, the strain within an element is
In matrix notation,
The stress in the element is given by
For our discretization, the element stresses are
A plot of this solution is shown in Figure 7.
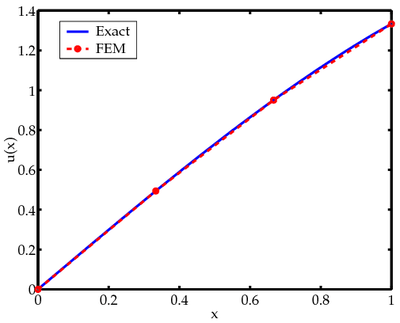 Figure 7(a). FEM vs exact solutions for displacements of an axially loaded bar. |
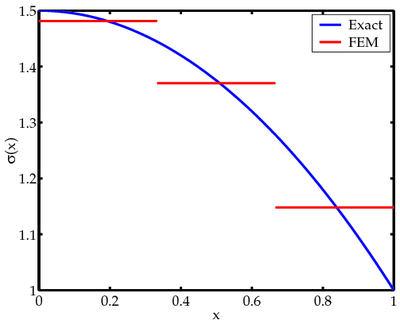 Figure 7(b). FEM vs exact solutions for stresses in an axially loaded bar. |
Matlab code
The finite element code (Matlab) used to compute this solution is given below.
function AxialBarFEM
A = 1.0;
L = 1.0;
E = 1.0;
a = 1.0;
R = 1.0;
e = 3;
h = L/e;
n = e+1;
for i=1:n
node(i) = (i-1)*h;
end
for i=1:e
elem(i,:) = [i i+1];
end
K = zeros(n);
f = zeros(n,1);
for i=1:e
node1 = elem(i,1);
node2 = elem(i,2);
Ke = elementStiffness(A, E, h);
fe = elementLoad(node(node1),node(node2), a, h);
K(node1:node2,node1:node2) = K(node1:node2,node1:node2) + Ke;
f(node1:node2) = f(node1:node2) + fe;
end
f(n) = f(n) + 1.0;
Kred = K(2:n,2:n);
fred = f(2:n);
d = inv(Kred)*fred;
dsol = [0 d'];
fsol = K*dsol';
sum(fsol)
figure;
p0 = plotDisp(E, A, L, R, a);
p1 = plot(node, dsol, 'ro--', 'LineWidth', 3); hold on;
legend([p0 p1],'Exact','FEM');
for i=1:e
node1 = elem(i,1);
node2 = elem(i,2);
u1 = dsol(node1);
u2 = dsol(node2);
[eps(i), sig(i)] = elementStrainStress(u1, u2, E, h);
end
figure;
p0 = plotStress(E, A, L, R, a);
for i=1:e
node1 = node(elem(i,1));
node2 = node(elem(i,2));
p1 = plot([node1 node2], [sig(i) sig(i)], 'r-','LineWidth',3); hold on;
end
legend([p0 p1],'Exact','FEM');
function [p] = plotDisp(E, A, L, R, a)
dx = 0.01;
nseg = L/dx;
for i=1:nseg+1
x(i) = (i-1)*dx;
u(i) = (1/6*A*E)*(-a*x(i)^3 + (6*R + 3*a*L^2)*x(i));
end
p = plot(x, u, 'LineWidth', 3); hold on;
xlabel('x', 'FontName', 'palatino', 'FontSize', 18);
ylabel('u(x)', 'FontName', 'palatino', 'FontSize', 18);
set(gca, 'LineWidth', 3, 'FontName', 'palatino', 'FontSize', 18);
function [p] = plotStress(E, A, L, R, a)
dx = 0.01;
nseg = L/dx;
for i=1:nseg+1
x(i) = (i-1)*dx;
sig(i) = (1/2*A*E)*(-a*x(i)^2 + (2*R + a*L^2));
end
p = plot(x, sig, 'LineWidth', 3); hold on;
xlabel('x', 'FontName', 'palatino', 'FontSize', 18);
ylabel('\sigma(x)', 'FontName', 'palatino', 'FontSize', 18);
set(gca, 'LineWidth', 3, 'FontName', 'palatino', 'FontSize', 18);
function [Ke] = elementStiffness(A, E, h)
Ke = (A*E/h)*[[1 -1];[-1 1]];
function [fe] = elementLoad(node1, node2, a, h)
x1 = node1;
x2 = node2;
fe1 = a*x2/(2*h)*(x2^2-x1^2) - a/(3*h)*(x2^3-x1^3);
fe2 = -a*x1/(2*h)*(x2^2-x1^2) + a/(3*h)*(x2^3-x1^3);
fe = [fe1;fe2];
function [eps, sig] = elementStrainStress(u1, u2, E, h)
B = [-1/h 1/h];
u = [u1; u2];
eps = B*u
sig = E*eps;
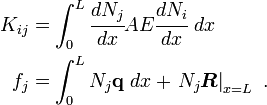
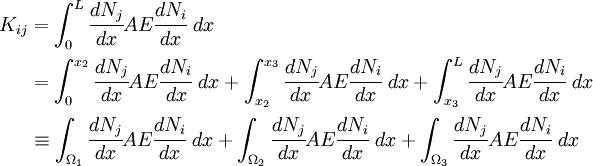
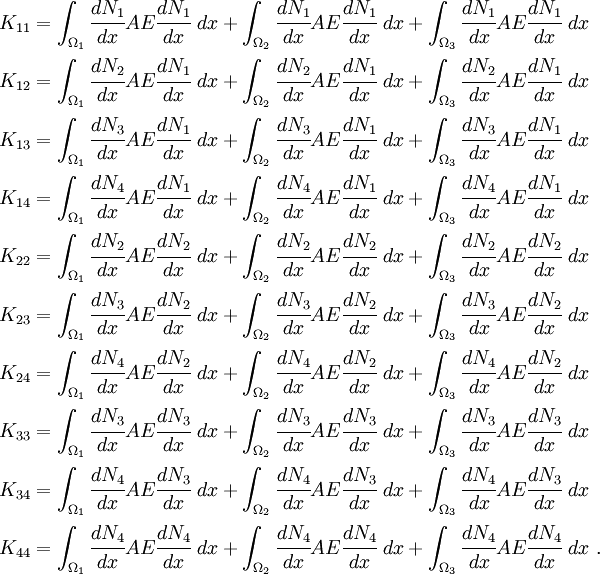
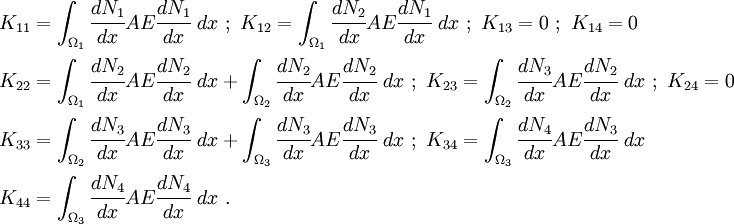
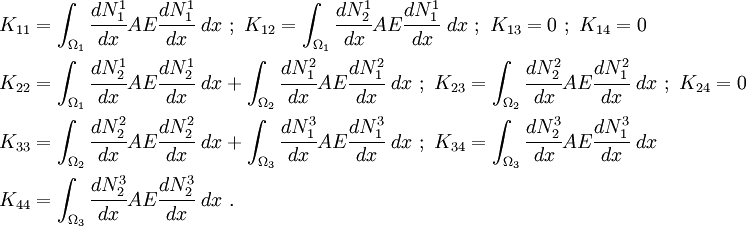
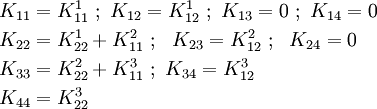
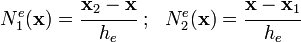
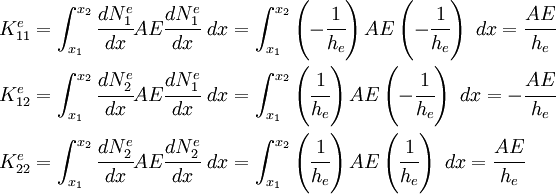
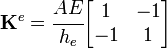
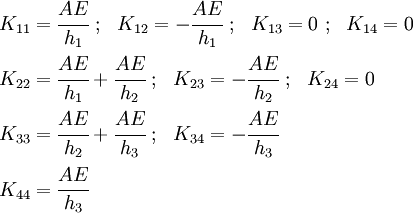
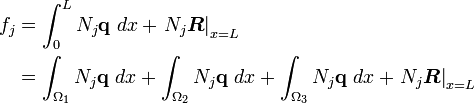
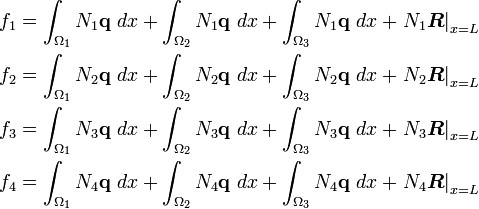
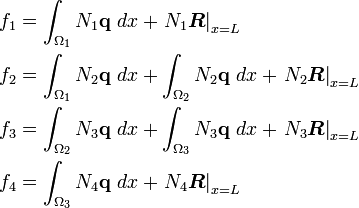
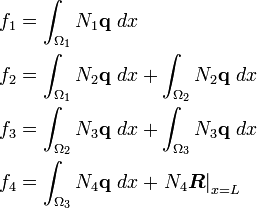


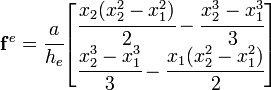
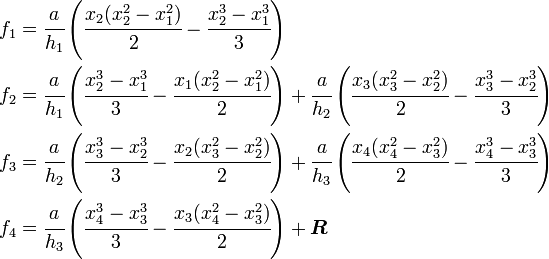
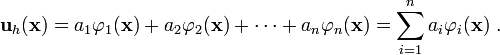
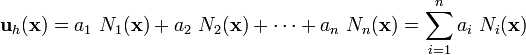
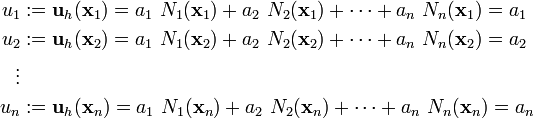
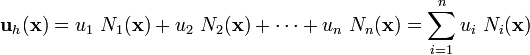

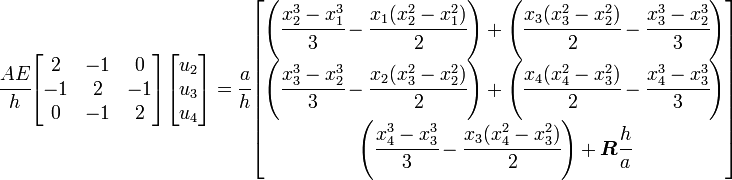
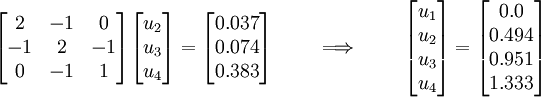
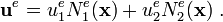
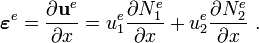
![\boldsymbol{\varepsilon}^e = \mathbf{B}^e \mathbf{u}^e
= \left[ \frac{\partial N^e_1}{\partial x} ~~ \frac{\partial N^e_2}{\partial x}\right]
\begin{bmatrix} u^e_1 \\ u^e_2 \end{bmatrix}
= \left[ -\cfrac{1}{h} ~~ \cfrac{1}{h} \right]
\begin{bmatrix} u^e_1 \\ u^e_2 \end{bmatrix}](../I/m/56b1f6cb64454c55ac81633f0a3fd445.png)