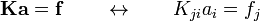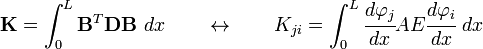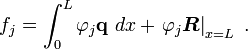Introduction to finite elements/Axial bar approximate solution
< Introduction to finite elementsApproximate Solution: The Galerkin Approach
To find the finite element solution, we can either start with the strong form and derive the weak form, or we can start with a weak form derived from a variational principle.
Let us assume that the approximate solution is  and plug
it into the ODE. We get
and plug
it into the ODE. We get
where 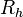 is the residual. We now try to minimize the residual in a weighted average sense
is the residual. We now try to minimize the residual in a weighted average sense
where 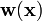 is a weighting function. Notice that this equation is similar to equation (5) (see 'Weak form: integral equation') with
is a weighting function. Notice that this equation is similar to equation (5) (see 'Weak form: integral equation') with 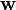 in place of the variation
in place of the variation 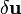 . For the two equations to be equivalent, the weighting function must also be such that
. For the two equations to be equivalent, the weighting function must also be such that 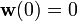 .
.
Therefore the approximate weak form can be written as
In Galerkin's method we assume that the approximate solution can be expressed as
In the Bubnov-Galerkin method, the weighting function is chosen to be of the same form as the approximate solution (but with arbitrary coefficients),
If we plug the approximate solution and the weighting functions into the approximate weak form, we get
This equation can be rewritten as
From the above, since 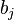 is arbitrary, we have
is arbitrary, we have
After reorganizing, we get
which is a system of 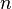 equations that can be solved for the unknown coefficients
equations that can be solved for the unknown coefficients 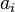 . Once we know the
. Once we know the 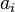 s, we can use them to compute approximate solution. The above equation can be written in matrix form as
s, we can use them to compute approximate solution. The above equation can be written in matrix form as
where
and
The problem with the general form of the Galerkin method is that the
functions 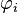 are difficult to determine for complex domains.
are difficult to determine for complex domains.
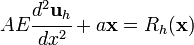
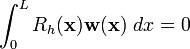
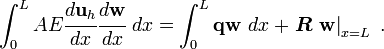
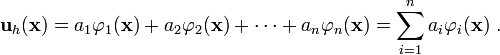
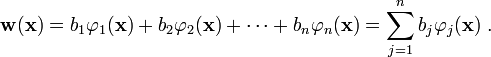
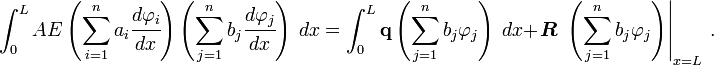
![\sum_{j=1}^n b_j
\left[\int_0^L AE \left(\sum_{i=1}^n a_i\cfrac{d\varphi_i}{dx}
\cfrac{d\varphi_j}{dx}\right)~dx
\right] = \sum_{j=1}^n b_j \left[\int_0^L\mathbf{q}\varphi_j~dx +
\left. \left(\boldsymbol{R}~\varphi_j\right)\right|_{x=L}\right] ~.](../I/m/e182b25a09de45abdc0edeefa988ce75.png)
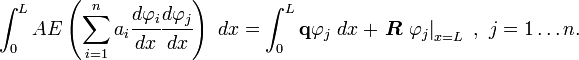
![\sum_{i=1}^n \left[\int_0^L \cfrac{d\varphi_j}{dx} AE
\cfrac{d\varphi_i}{dx}~dx\right] a_i =
\int_0^L \varphi_j\mathbf{q}~dx + \left. \varphi_j\boldsymbol{R}\right|_{x=L} ~,
~ j = 1\dots n](../I/m/7080b2c6318f0841bdc913719dcae4b2.png)