Introduction to Statistics/Still confused?

< Introduction to Statistics

Consider a simpler situation involving a deck of two cards: the queen of spades and the two of spades. We'll define our joint probability again as "the chance of drawing a queen or a spade", and naively express it as.
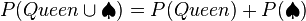
$P(Queen \cup \spadesuit) = P(Queen) + P(\spadesuit)$
We can draw a card from our two card deck. We are guaranteed to draw a spade, so 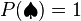$P(\spadesuit) = 1$ . Our chance of drawing a queen is 1 in 2, or 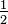$\tfrac{1}{2}$ . Let's add everything together. 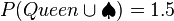$P(Queen \cup \spadesuit) = 1.5$ or 150%. This obviously doesn't make sense.

If we use the correct definition of the probability for this event:
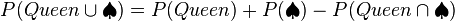
$P(Queen \cup \spadesuit) = P(Queen) + P(\spadesuit) - P(Queen \cap \spadesuit)$
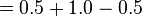
$= 0.5 + 1.0 - 0.5$
we get the answer we expect.

This article is issued from Wikiversity - version of the Saturday, September 28, 2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.