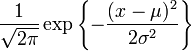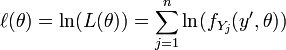Introduction to Likelihood Theory/Maximum Likelihood Estimation

< Introduction to Likelihood Theory

A simple idea: Since we have seen in previous section (Intuitive Meaning?), we may regard likelihood as the probability of the sample 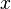$x$ showing up in the space of all the possibles samples of size 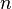$n$ for a given value of 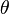$\theta$ . But the sample 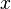$x$ has actually occurred and the sample space is infinite, so this sample might have something special - perhaps it's probability of showing up is bigger than the others. Why don't we maximize it?

Maximizing the Likelihood

If we try to maximize likelihoods of variables with densities like the Gaussian

\frac{1}{\sqrt{2\pi}}\exp\left\{-\frac{(x-\mu)^{2}}{2\sigma^{2}}\right\}

directly, things can be rather complicated. But, we know from calculus that maximizing (or minimizing) 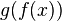$g(f(x))$ when $g$ is strictly crescent is equivalent to maximizing 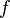$f$ . So, we take the logarithm of the likelihood and call the function

\ell(\theta)=\ln(L(\theta))=\sum_{j=1}^{n}\ln(f_{Y_{j}}(y',\theta))

log-likelihood. So, we will maximize the log-likelihood instead of maximizing the proper likelihood.

Statistics, Estimators, Unbiased Estimators, Variance and Consistency of an Estimator

A statistic is a function from a sample 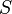$S$ in any space we are interested, and suppose that there a log-likelihood function 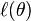$\ell(\theta)$ ; A estimator for 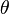$\theta$ is a statistic used to estimate 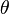$\theta$ . These definitions don't add much, but since these words are commonplace for staticians worldwide, they are worth defining. Note that any statistic or estimator is itself a random variable.

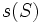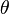In this section we will use our previous notation for samples. A estimator $s(S)$ for $\theta$ is called unbiased if $E[s]=\theta$ , and asymptotically unbiased if

$\lim_{n\rightarrow \infty} E[s(S_{n})]=\theta$

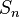where $S_{n}$ is a sequence of samples(as defined in the section about sampling). In classical views of statistics, only estimators that possessed at least one of these properties where admissible, but the Maximum Likehood Estimators (MLE) are not necessarily unbiased nor asymptotically unbiased.

TODO: Examples of biased estimatives (the easier one is the variance of a normal distribution).

The variance of a estimator $s$ is another important thing; We expect that, as our data grows in size, the variance of the estimator goes to zero, for more data means more information, more information means more certanity. So, we say that the estimator is consistent if

$\lim_{n\rightarrow \infty} V[s(S_{n})]=0$

but such a strong condition is rarely satisfied; Usually, we have to contempt ourselves with weakly consistent estimators, estimators where

$V[s(S_{n})]=O_{p}(n^{-1})$

Reparametrization and Invariance

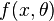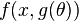TODO: Show how to reparametrize a gaussian using the coefficient of variation instead of the variance. Show how to reparametrize $f(x,\theta)$ to $f(x,g(\theta))$ .

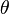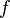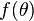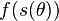A estimator $s$ of $\theta$ is called invariant under the transformation $f$ if the estimator of the parameter $f(\theta)$ is $f(s(\theta))$ . One important property of maximum likelihood estimators is that they are invariant under strictly monotone transformations.

TODO: Show estimators that aren't invariant under monotone functions.

Properties of Maximum Likelihood Estimates

TODO: Show that the MLE are consistent.

Examples of finding Maximum Likelihood Estimators

TODO: Example with a single parameter, continuous case.

TODO: Example of discrete case. Mark-Recapture Sampling.

A wildlife biologist captures and tags n1=300 ducks, and then releases them. After allowing time for mixing of the tagged birds with the population, a second sample of n2=200 birds is taken. It is found that m2=10 of these birds are found to be tagged.

Write down a binomial likelihood for m2.

Plot the likelihood of m2 as a function of the population abundance, N.

What is a maximum likelihood estimator of N?

TODO: Example with a two or more parameters, continuous case. that is nothing

TODO: Example Finding MLE's with a numerical method.

Often in applied problems the likelihood is so complicated that a closed form solution for the MLE cannot be found. In such cases, one must use numerical methods to find an approximate solution. The Metropolis Algorithm is a commonly used approach.

This article is issued from Wikiversity - version of the Saturday, February 15, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.