Introduction to Elasticity/Wedge with boundary tractions
< Introduction to ElasticityWedge with Boundary Tractions
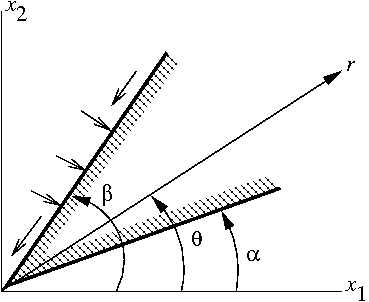 Elastic wedge with normal and shear surface tractions |
Suppose
- The tractions on the boundary vary as
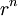 .
. - No body forces.
Then
To find 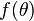 plug into
plug into 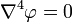 .
.
If 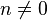 and
and 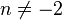 ,
,
The corresponding stresses and displacements can be found from the tables associated with Michell's solution. We have to take special care for the case where
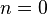 , i.e., the traction on the surface is constant.
, i.e., the traction on the surface is constant.
Sample Homework Problem
Find the stresses and displacements for a wedge loaded in constant shear 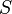 on its surface.
on its surface.
This article is issued from Wikiversity - version of the Saturday, February 13, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
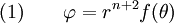
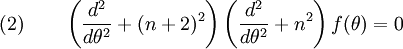
![\text{(3)} \qquad
\varphi = r^{n+2} \left[ a_1 \cos\{(n+2)\theta\} +
a_2 \cos(n\theta) + a_3 \sin\{(n+2)\theta\} + a_4 \sin(n\theta)\right]](../I/m/19e6e3ea188503170271383f165e45ef.png)