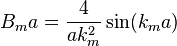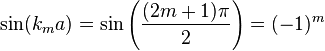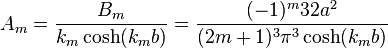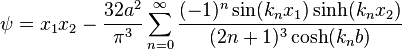Introduction to Elasticity/Warping of rectangular cylinder
< Introduction to ElasticityExample 3: Rectangular Cylinder
In this case, the form of 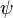 is not obvious and has to be
derived from the traction-free BCs
is not obvious and has to be
derived from the traction-free BCs
Suppose that 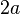 and
and 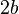 are the two sides of the rectangle, and
are the two sides of the rectangle, and 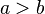 .
Also
.
Also 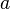 is the side parallel to
is the side parallel to 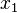 and
and 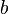 is the side parallel to
is the side parallel to  .
Then, the traction-free BCs are
.
Then, the traction-free BCs are
A suitable 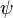 must satisfy these BCs and
must satisfy these BCs and 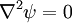 .
.
We can simplify the problem by a change of variable
Then the equilibrium condition becomes
The traction-free BCs become
Let us assume that
Then,
or,
Case 1: 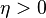 or
or 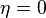
In both these cases, we get trivial values of 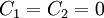 .
.
Case 2: 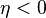
Let
Then,
Therefore,
Apply the BCs at 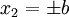 ~~ (
~~ (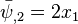 ), to get
), to get
or,
The RHS of both equations are odd. Therefore, 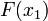 is odd. Since,
is odd. Since,
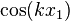 is an even function, we must have
is an even function, we must have 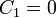 .
.
Also,
Hence, 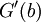 is even. Since
is even. Since 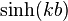 is an odd function, we must
have
is an odd function, we must
have 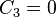 .
.
Therefore,
Apply BCs at 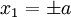 (
(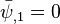 ), to get
), to get
The only nontrivial solution is obtained when 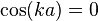 , which means that
, which means that
The BCs at 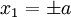 are satisfied by every terms of the series
are satisfied by every terms of the series
Applying the BCs at 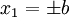 again, we get
again, we get
Using the orthogonality of terms of the sine series,
we have
or,
Now,
Therefore,
The warping function is
The torsion constant and the stresses can be calculated from 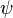 .
.
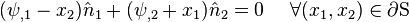
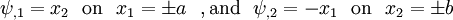
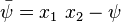
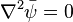
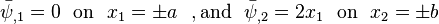
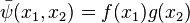
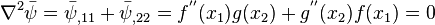
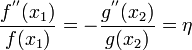
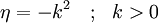
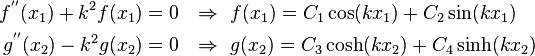
![\bar{\psi}(x_1,x_2) = \left[ C_1 \cos(kx_1) + C_2 \sin(kx_1) \right]
\left[ C_3 \cosh(kx_2) + C_4 \sinh(kx_2) \right]](../I/m/fd0bcf5d3b6e34609e5ab90b7e685535.png)
![\begin{align}
\left[ C_1 \cos(kx_1) + C_2 \sin(kx_1) \right]
\left[ C_3 \sinh(kb) + C_4 \cosh(kb) \right] & = 2x_1\\
\left[ C_1 \cos(kx_1) + C_2 \sin(kx_1) \right]
\left[-C_3 \sinh(kb) + C_4 \cosh(kb) \right] & = 2x_1
\end{align}](../I/m/4a65d8cfef3d0ea3436658f3f76aa7e8.png)
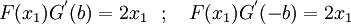
![F(x_1) \left[ G^{'}(b) - G^{'}(-b)\right] = 0](../I/m/b4ba714fb1e12d9fbdfbc6788fc8d5b3.png)
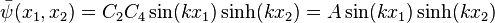
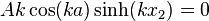
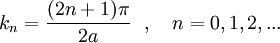
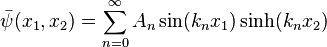
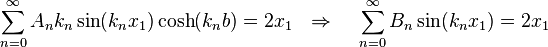
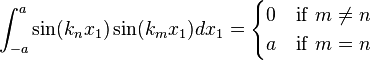
![\int_{-a}^a \left[\sum_{n=0}^{\infty} B_n \sin(k_n x_1)\right]
\sin(k_m x_1) dx_1 =
\int_{-a}^a \left[2 x_1\right] \sin(k_m x_1) dx_1](../I/m/a3e8b5051f26c66c732beb320dfe9f97.png)