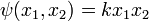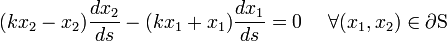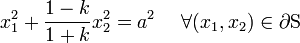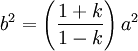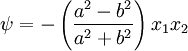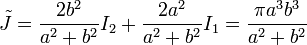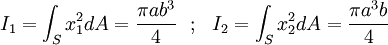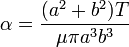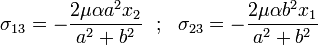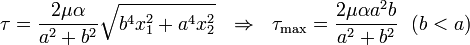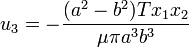Introduction to Elasticity/Warping of elliptical cylinder
< Introduction to ElasticityExample 2: Elliptical Cylinder
Choose warping function
where 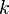 is a constant.
is a constant.
Equilibrium (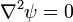 ) is satisfied.
) is satisfied.
The traction free BC is
Integrating,
where 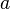 is a constant.
is a constant.
This is the equation for an ellipse with major and minor axes 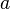 and
and 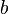 ,
where
,
where
The warping function is
The torsion constant is
where
If you compare 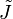 and
and 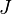 for the ellipse, you will find that
for the ellipse, you will find that 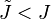 . This implies that the torsional rigidity is less than that predicted with the assumption that plane sections remain plane.
. This implies that the torsional rigidity is less than that predicted with the assumption that plane sections remain plane.
The twist per unit length is
The non-zero stresses are
The projected shear traction is
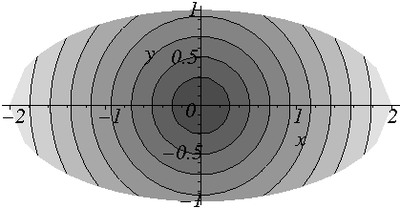 Shear stresses in the cross section of an elliptical cylinder under torsion |
For any torsion problem where 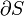 is convex, the maximum projected shear traction occurs at the point on
is convex, the maximum projected shear traction occurs at the point on 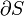 that is nearest the centroid of
that is nearest the centroid of 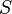 .
.
The displacement 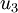 is
is
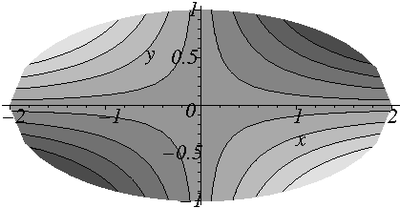 Displacements ( 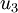 ) in the cross section of an elliptical cylinder under torsion ) in the cross section of an elliptical cylinder under torsion |
This article is issued from Wikiversity - version of the Wednesday, August 08, 2007. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.