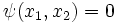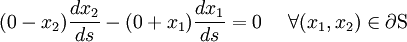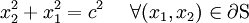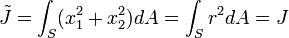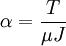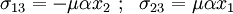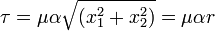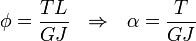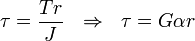Introduction to Elasticity/Warping of circular cylinder

Example 1: Circular Cylinder

Choose warping function

\psi(x_1,x_2) = 0 \,

Equilibrium (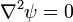 $\nabla^2{\psi} = 0$ ) is trivially satisfied.

The traction free BC is

(0 - x_2) \frac{dx_2}{ds} - (0 + x_1) \frac{dx_1}{ds} = 0 ~~~~ \forall (x_1, x_2) \in \partial\text{S}

Integrating,

x_2^2 + x_1^2 = c^2 ~~~~ \forall (x_1, x_2) \in \partial\text{S}

where $c$ is a constant.

Hence, a circle satisfies traction-free BCs.

There is no warping of cross sections for circular cylinders

The torsion constant is

\tilde{J} = \int_S (x_1^2 + x_2^2) dA = \int_S r^2 dA = J

The twist per unit length is

\alpha = \frac{T}{\mu J}

The non-zero stresses are

\sigma_{13} = -\mu\alpha x_2 ~;~~ \sigma_{23} = \mu\alpha x_1

The projected shear traction is

\tau = \mu\alpha\sqrt{(x_1^2 + x_2^2)} = \mu\alpha r

Compare results from Mechanics of Materials solution

\phi = \frac{TL}{GJ} ~~\Rightarrow~~ \alpha = \frac{T}{GJ}

and

\tau = \frac{Tr}{J} ~~\Rightarrow~~ \tau = G\alpha r

This article is issued from Wikiversity - version of the Wednesday, August 08, 2007. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.