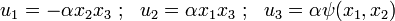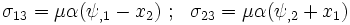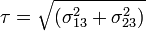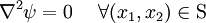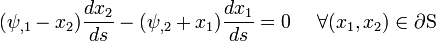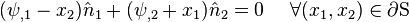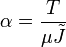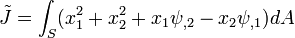Introduction to Elasticity/Warping functions

Warping Function and Torsion of Non-Circular Cylinders

Warping functions are quite useful in the solution of problems involving the torsion of cylinders with non-circular cross sections.

For such problems, the displacements are given by

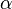u_1 = -\alpha x_2 x_3 ~;~~ u_2 = \alpha x_1 x_3 ~;~~ u_3 = \alpha\psi(x_1,x_2)

where $\alpha\,$ is the twist per unit length, and 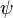$\psi\,$ is the warping function.

The stresses are given by

\sigma_{13} = \mu\alpha(\psi_{,1} - x_2) ~;~~ \sigma_{23} = \mu\alpha(\psi_{,2} + x_1)

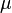where $\mu\,$ is the shear modulus.

The projected shear traction is

\tau = \sqrt{(\sigma_{13}^2 + \sigma_{23}^2)}

Equilibrium is satisfied if

\nabla^2{\psi} = 0 ~~~~ \forall (x_1, x_2) \in \text{S}

Traction-free lateral BCs are satisfied if

(\psi_{,1} - x_2) \frac{dx_2}{ds} - (\psi_{,2} + x_1) \frac{dx_1}{ds} = 0 ~~~~ \forall (x_1, x_2) \in \partial\text{S}

or,

(\psi_{,1} - x_2) \hat{n}_{1} + (\psi_{,2} + x_1) \hat{n}_{2} = 0 ~~~~ \forall (x_1, x_2) \in \partial\text{S}

The twist per unit length is given by

\alpha = \frac{T}{\mu \tilde{J}}

where the torsion constant

\tilde{J} = \int_S (x_1^2 + x_2^2 + x_1\psi_{,2} - x_2\psi_{,1}) dA

This article is issued from Wikiversity - version of the Saturday, February 13, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.