Introduction to Elasticity/Transversely loaded wedge
< Introduction to ElasticitySample homework problems
Wedge loaded transversely by a concentrated load
Given:
A wedge of infinite length with a concentrated load 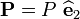 per
unit wedge thickness at the vertex. Plane stress/strain.
per
unit wedge thickness at the vertex. Plane stress/strain.
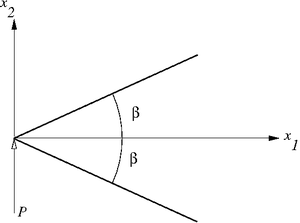 Wedge loaded transversely by a concentrated load |
Find:
The stress field in the wedge.
Solution
From the Flamant solution, we know that the stress field in the wedge is
The constants 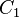 and
and 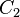 can be found by using the equilibrium
conditions
can be found by using the equilibrium
conditions
or,
Therefore,
Hence, the stresses are
This article is issued from Wikiversity - version of the Monday, February 01, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
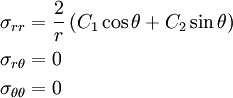
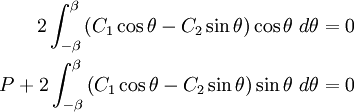
![\begin{align}
C_1 \left[2\beta + \sin(2\beta)\right] & = 0 \\
P + C_2\left[\sin(2\beta) - 2 \beta\right] & = 0
\end{align}](../I/m/83c3eeecc9529d6d39a30a58b3db9dd2.png)
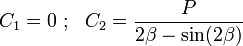
![\begin{align}
\sigma_{rr} & = \frac{2P\sin\theta}{r\left[2\beta-\sin(2\beta)\right]}\\
\sigma_{r\theta} & = 0 \\
\sigma_{\theta\theta} & = 0
\end{align}](../I/m/b126ab3e7bc7b0e5eebd05a8e6ff09e5.png)