Introduction to Elasticity/Transformation example 1
< Introduction to ElasticityExample 1
Derive the transformation rule for second order tensors
(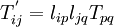 ). Express this relation in matrix notation.
). Express this relation in matrix notation.
Solution
A second-order tensor 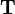 transforms a vector
transforms a vector 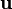 into another vector
into another vector 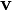 .
Thus,
.
Thus,
In index and matrix notation,
Let us determine the change in the components of 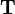 with change the basis
from (
with change the basis
from (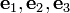 ) to (
) to (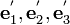 ). The vectors
). The vectors 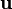 and
and 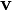 , and
the tensor
, and
the tensor 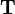 remain the same. What changes are the components with respect
to a given basis. Therefore, we can write
remain the same. What changes are the components with respect
to a given basis. Therefore, we can write
Now, using the vector transformation rule,
Plugging the first of equation (3) into equation (2) we get,
Substituting for 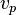 in equation~(4) using equation~(1),
in equation~(4) using equation~(1),
Substituting for 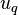 in equation (5) using equation (3),
in equation (5) using equation (3),
Therefore, if ![\mathbf{u} \equiv \left[u\right]](../I/m/f4f0bb802cec8ae32902a1c2168270c4.png) is an arbitrary vector,
is an arbitrary vector,
which is the transformation rule for second order tensors.
Therefore, in matrix notation, the transformation rule can be written as
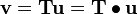
![\text{(1)} \qquad
v_i = T_{ij} u_i \leftrightarrow v_p = T_{pq} u_q ~\text{or,}~
\left[v\right] = \left[T\right] \left[u\right]](../I/m/8472295d614519f54cfe54d2f694ac6f.png)
![\text{(2)} \qquad
v^{'}_i = T^{'}_{ij} u^{'}_i ~\text{or,}~
\left[v\right]^{'} = \left[T\right]^{'} \left[u\right]^{'}](../I/m/ccd2be2cec8984ff5a3482153509024f.png)
![\begin{align}\text{(3)} \qquad
v^{'}_i & = l_{ip} v_p ~;~ u^{'}_i = l_{ip} u_p ~\text{or,}~
\left[v\right]^{'} = \left[L\right] \left[v\right] ~; \left[u\right]^{'} = \left[L\right] \left[u\right] \\
v_q & = l_{iq} v^{'}_i ~;~ u_q = l_{iq} u^{'}_i ~\text{or,}~
\left[v\right] = \left[L\right]^{T} \left[v\right]^{'} ~; \left[u\right] = \left[L\right]^{T} \left[u\right]^{'}
\end{align}](../I/m/f6eb1e493c2994ff216fab847ee0a49a.png)
![\text{(4)} \qquad
l_{ip} v_p = T^{'}_{ij} u^{'}_i ~\text{or,}~
\left[L\right] \left[v\right] = \left[T\right]^{'} \left[u\right]^{'}](../I/m/30ce5b4d9f29bba8d07920a3b875eda8.png)
![\text{(5)} \qquad
l_{ip} T_{pq} u_q = T^{'}_{ij} u^{'}_i ~\text{or,}~
\left[L\right] \left[T\right] \left[u\right] = \left[T\right]^{'} \left[u\right]^{'}](../I/m/6231cfde05b3b830fc0d76e38a05e82d.png)
![\text{(6)} \qquad
l_{ip} T_{pq} l_{iq} u^{'}_i = T^{'}_{ij} u^{'}_i ~\text{or,}~
\left[L\right] \left[T\right] \left[L\right]^{T} \left[u\right]^{'} = \left[T\right]^{'} \left[u\right]^{'}](../I/m/8c496efea22b4268662e20c4f72bd7ed.png)
![l_{ip} T_{pq} l_{iq} = T^{'}_{ij} \Rightarrow
T^{'}_{ij} = l_{ip} l_{jq} T_{pq} ~\text{or,}~
\left[T\right]^{'} = \left[L\right] \left[T\right] \left[L\right]^{T}](../I/m/39114a881060e7add8fc9dfc2a2c6e65.png)
![\left[T\right]^{'} = \left[L\right] \left[T\right] \left[L\right]^{T}](../I/m/ad60b8737db287a62aa5f1e2c05b4cb0.png)