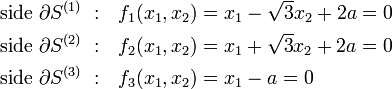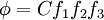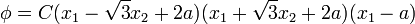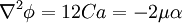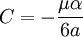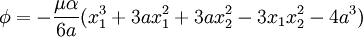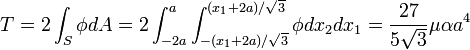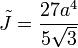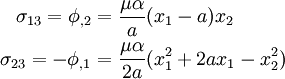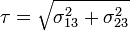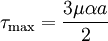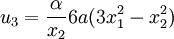Introduction to Elasticity/Torsion of triangular cylinder
< Introduction to ElasticityExample: Equilateral Triangle
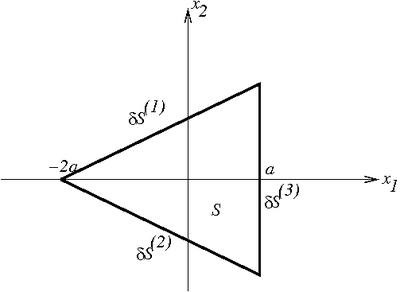 Torsion of a cylinder with a triangular cross section |
The equations of the three sides are
Let the Prandtl stress function be
Clearly, 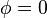 at the boundary of the cross-section (which is what we need for solid cross sections).
at the boundary of the cross-section (which is what we need for solid cross sections).
Since, the traction-free boundary conditions are satisfied by 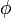 , all we have to do is satisfy the compatibility condition to get the value of
, all we have to do is satisfy the compatibility condition to get the value of  . If we can get a closed for solution for
. If we can get a closed for solution for 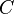 , then the stresses derived from
, then the stresses derived from 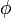 will satisfy equilibrium.
will satisfy equilibrium.
Expanding 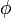 out,
out,
Plugging into the compatibility condition
Therefore,
and the Prandtl stress function can be written as
The torque is given by
Therefore, the torsion constant is
The non-zero components of stress are
The projected shear stress
is plotted below
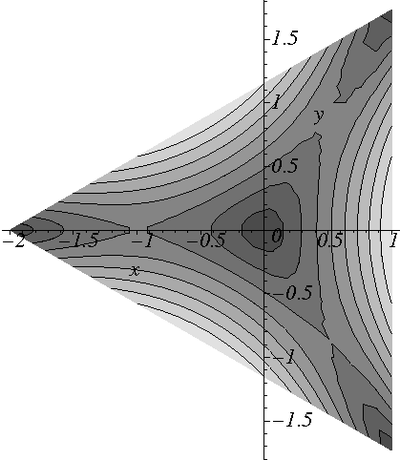 Stresses in a cylinder with a triangular cross section under torsion |
The maximum value occurs at the middle of the sides. For example,
at 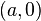 ,
,
The out-of-plane displacements can be obtained by solving for the
warping function 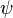 . For the equilateral triangle, after some
algebra, we get
. For the equilateral triangle, after some
algebra, we get
The displacement field is plotted below
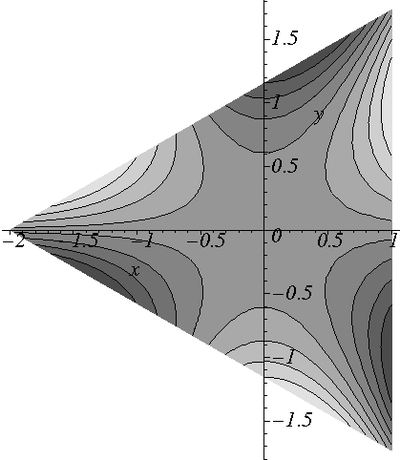 Displacements 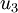 in a cylinder with a triangular cross section. in a cylinder with a triangular cross section. |