Introduction to Elasticity/Torsion of rectangular sections
< Introduction to ElasticitySample homework problem
Torsion of a bar with a rectangular cross section
Given:
A cylinder with a rectangular cross sections 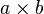 under torison.
under torison.
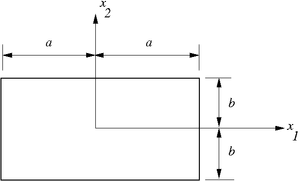 A bar with a rectangular cross section |
Show:
Why a function of the form
cannot be used as a Prandtl stress function for this cross section.
Solution
For compatibility, we need
However, for the given 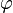 ,
,
which is not constant. Hence, the given function cannot be used as a Prandtl stress function.
This article is issued from Wikiversity - version of the Monday, February 01, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
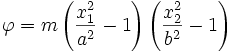
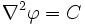
![\nabla^2{\varphi} = -\frac{2m}{a^2b^2}\left[a^2+b^2-(x_1^2+x_2^2)\right]](../I/m/af93b7f5a5258eabfb2d5b41d216b2e8.png)