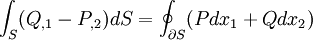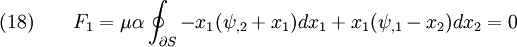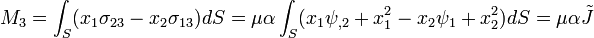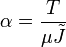Introduction to Elasticity/Torsion of noncircular cylinders
< Introduction to ElasticityTorsion of Non-Circular Cylinders
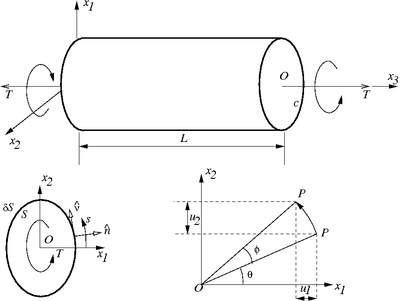 Torsion of a noncircular cylinder |
About the problem
- Solution first found by St. Venant.
- Tractions at the ends are statically equivalent to equal and opposite torques
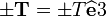 .
. - Lateral surfaces are traction-free.
Assumptions:
- An axis passes through the center of twist (
 axis).
axis). - Each c.s. projection on to the
 plane rotates,but remains undistorted.
plane rotates,but remains undistorted. - The rotation of each c.s. (
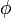 ) is proportional to
) is proportional to 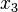 .
.
where 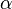 is the twist per unit length.
is the twist per unit length.
- The out-of-plane distortion (warping) is the same for each c.s. and is proportional to
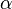 .
.
Find:
- Torsional rigidity (
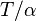 ).
). - Maximum shear stress.
Solution:
Displacements
where 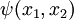 is the warping function.
is the warping function.
If 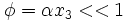 (small strain),
(small strain),
Strains
Therefore,
Stresses
Therefore,
Equilibrium
Therefore,
Internal Tractions
- Normal to cross sections is
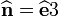 .
. - Normal traction
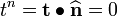 .
. - Projected shear traction is
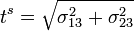 .
. - Traction vector at a point in the cross section is tangent to the cross section.
Boundary Conditions on Lateral Surfaces
- Lateral surface traction-free.
- Unit normal to lateral surface appears as an in-plane unit normal to the boundary
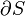 .
.
We parameterize the boundary curve 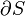 using
using
The tangent vector to  is
is
The tractions 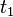 and
and 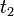 on the lateral surface are identically zero.
However, to satisfy the BC
on the lateral surface are identically zero.
However, to satisfy the BC 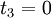 , we need
, we need
or,
Boundary Conditions on End Surfaces
The traction distribution is statically equivalent to the torque 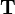 .
At
.
At 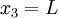 ,
,
Therefore,
From equilibrium,
Hence,
The Green-Riemann Theorem
If 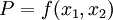 and
and 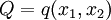 then
then
with the integration direction such that 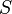 is to the left.
is to the left.
Applying the Green-Riemann theorem to equation (17), and using equation (16)
Similarly, we can show that 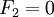 .
. 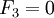 since
since 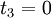 .
.
The moments about the 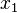 and
and  axes are also zero.
axes are also zero.
The moment about the 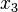 axis is
axis is
where 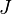 is the torsion constant. Since
is the torsion constant. Since 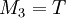 , we have
, we have
If 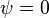 , then
, then 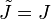 , the polar moment of inertia.
, the polar moment of inertia.
Summary of the solution approach
- Find a warping function
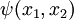 that is harmonic. and satisfies the traction BCs.
that is harmonic. and satisfies the traction BCs. - Compatibility is not an issue since we start with displacements.
- The problem is independent of applied torque and the material properties of the cylinder.
- So it is just a geometrical problem. Once
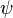 is known, we can calculate
is known, we can calculate
- The displacement field.
- The stress field.
- The twist per unit length.
This article is issued from Wikiversity - version of the Monday, February 01, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
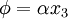
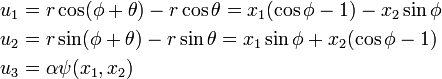
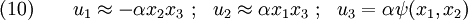
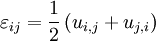
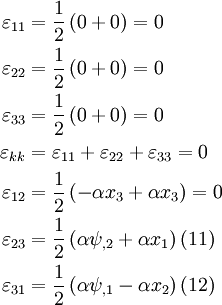
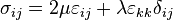
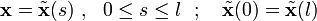
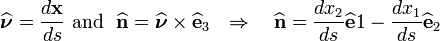
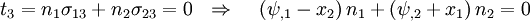
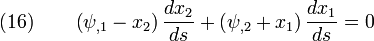
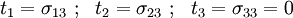
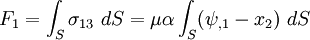
![\begin{align}
\nabla^2{\psi} = 0 ~~\Rightarrow~~~
\psi_{,1}-x_2 & = (\psi_{,1}-x_2) + x_1(\psi_{,11} + \psi_{,22}) \\
& = \psi_{,1} + x_1\psi_{,11} - x_2 + x_1\psi_{,22} \\
& = (x_1\psi_{,1} - x_1x_2)_{,1} + (x_1\psi_{,2} + x_1x_1)_{,2} \\
& = \left[x_1(\psi_{,1} - x_2)\right]_{,1} +
\left[x_1(\psi_{,2} + x_1)\right]_{,2}
\end{align}](../I/m/b57d297680179ed36c459a903ab6ce30.png)
![\text{(17)} \qquad
F_1 = \mu\alpha\int_S\left[x_1(\psi_{,1} - x_2)\right]_{,1} +
\left[x_1(\psi_{,2} + x_1)\right]_{,2} dS](../I/m/fbac35ffdbd15cdfba233818a8573765.png)