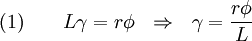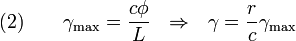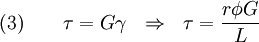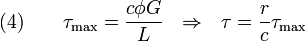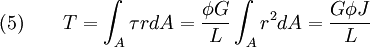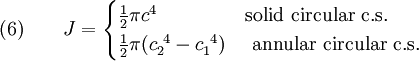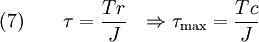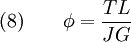Introduction to Elasticity/Torsion of circular cylinders

< Introduction to Elasticity

Torsion of Circular Cylinders

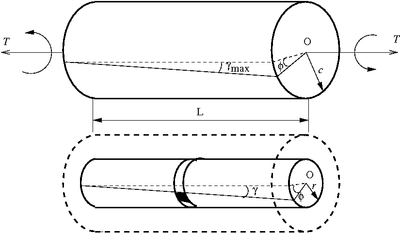Torsion of a cylinder with a circular cross section

About the problem:

Circular Cylinder.
Centroidal axis thru the center of each cross section (c.s.)
Length 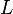$L$ , Outer radius $c$ .
Applied torque $T$ .
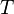Angle of twist $\phi$ .

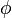Assumptions:

Each c.s. remains plane and undistorted.
Each c.s. rotates through the same angle.
No warping or change in shape.
Amount of displacement of each c.s. is proportional to distance from end.

Find:

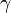Shear strains in the cylinder ( $\gamma$ ).
Shear stress in the cylinder ( $\tau$ ).
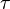Relation between torque ( 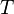$T$ ) and angle of twist ( $\phi$ ).
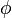Relation between torque ( 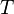$T$ ) and shear stress ( $\tau$ ).

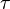Solution:

If 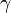$\gamma$ is small, then

\text{(1)} \qquad L\gamma = r\phi ~~\Rightarrow~~ {\gamma = \frac{r\phi}{L}}

Therefore,

\text{(2)} \qquad \gamma_{\text{max}} = \frac{c\phi}{L} ~~\Rightarrow~~ \gamma = \frac{r}{c} \gamma_{\text{max}}

If the material is linearly elastic,

\text{(3)} \qquad \tau = G\gamma ~~\Rightarrow~~ {\tau = \frac{r\phi G}{L}}

Therefore,

\text{(4)} \qquad \tau_{\text{max}} = \frac{c\phi G}{L} ~~\Rightarrow~~ \tau = \frac{r}{c} \tau_{\text{max}}

The torque on each c.s. is given by

\text{(5)} \qquad T = \int_A \tau r dA = \frac{\phi G}{L}\int_A r^2 dA = \frac{G\phi J}{L}

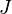where $J$ is the polar moment of inertia of the c.s.

\text{(6)} \qquad J = \begin{cases} \frac{1}{2} \pi c^4 & \text{solid circular c.s.} \\ \frac{1}{2} \pi (c_2^{~4}-c_1^{~4}) & \text{ annular circular c.s.} \end{cases}

Therefore,

\text{(7)} \qquad {\tau = \frac{Tr}{J}} ~~\Rightarrow \tau_{\text{max}} = \frac{Tc}{J}

and

\text{(8)} \qquad {\phi = \frac{TL}{JG}}

This article is issued from Wikiversity - version of the Monday, February 01, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.