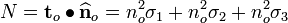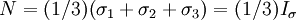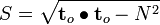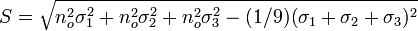Introduction to Elasticity/Stress example 4
< Introduction to ElasticityExample 4
Given:
The octahedral plane is the plane that is equally inclined to the directions of the three principal stresses. For any given stress of state there are eight such planes.
Show:
- The normal traction on an octahedral plane is given by
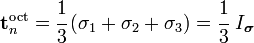 .
. - The projected shear traction on an octahedral plane is given by
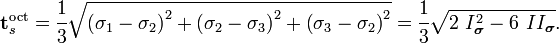
Here 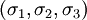 are the principal stresses and
are the principal stresses and 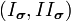 are the first two invariants of the stress tensor (
are the first two invariants of the stress tensor (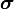 ).
).
Solution
Let us take the basis as the directions of the principal stresses
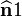 ,
, 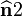 ,
, 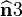 . Then the stress tensor is given by
. Then the stress tensor is given by
If 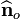 is the direction of the normal to an octahedral plane, then the components of this normal with respect to the principal basis are
is the direction of the normal to an octahedral plane, then the components of this normal with respect to the principal basis are 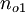 ,
, 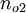 , and
, and 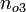 . The normal is
oriented in such a manner that it makes equal angles with the principal directions. Therefore,
. The normal is
oriented in such a manner that it makes equal angles with the principal directions. Therefore, 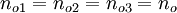 . Since
. Since 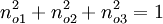 , we have
, we have 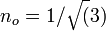 .
.
The traction vector on an octahedral plane is given by
The normal traction is,
Now, 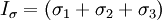 . Therefore,
. Therefore,
The projected shear traction is given by
Therefore,
Also,
If you do the algebra for S, you will get the required relations.
![\left[\boldsymbol{\sigma}\right] =
\begin{bmatrix}
\sigma_1 & 0 & 0 \\ 0 & \sigma_2 & 0 \\ 0 & 0 & \sigma_3
\end{bmatrix}](../I/m/fb456f706d56075d29af5908ca432839.png)
![\mathbf{t}_o = \widehat{\mathbf{n}}_{o} \bullet \left[\boldsymbol{\sigma}\right] = {n_o \sigma_1, n_o \sigma_2, n_o \sigma_3}](../I/m/3ad5629c35051872d9ec5c3bae1d3f2e.png)