Introduction to Elasticity/Stress example 2
< Introduction to ElasticityExample 2
Given:
A homogeneous stress field with components in the basis 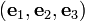 given by
given by
Find:
- The traction (
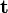 ) acting on a surface with unit normal
) acting on a surface with unit normal 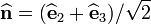 .
. - The normal traction (
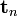 ) acting on a surface with unit normal
) acting on a surface with unit normal 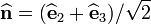 .
. - The projected shear traction (
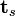 ) acting on a surface with unit normal
) acting on a surface with unit normal 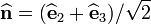 .
. - The principal stresses.
- The principal directions of stress.
Solution
Here's how you can solve this problem using Maple.
with(linalg):
sigma := linalg[matrix](3,3,[3,1,1,1,0,2,1,2,0]);
e2 := linalg[matrix](3,1,[0,1,0]);
e3 := linalg[matrix](3,1,[0,0,1]);
n := evalm((e2+e3)/sqrt(2));
sigmaT := transpose(sigma);
t := evalm(sigmaT&*n);
tT := transpose(t);
N := evalm(tT&*n);
tdott := evalm(tT&*t);
S := sqrt(tdott[1,1] - N[1,1]^2);
sigPrin := eigenvals(sigma);
dirPrin := eigenvects(sigma);
dirPrin[1];
dirPrin[2];
dirPrin[3];
This article is issued from Wikiversity - version of the Monday, February 01, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
![\left[\boldsymbol{\sigma}\right] =
\begin{bmatrix}
3 & 1 & 1 \\ 1 & 0 & 2 \\ 1 & 2 & 0
\end{bmatrix}
\text{(MPa)}](../I/m/83780a1ab516e20ceb8c21ab02df47d8.png)
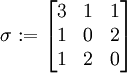
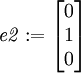
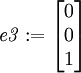
![n := \begin{bmatrix} 0 \\
{ \frac {\sqrt{2}}{2}} \\ [2ex]
{ \frac {\sqrt{2}}{2}}
\end{bmatrix}](../I/m/56ff37f6bd67b99c2068f41d406bc8c6.png)
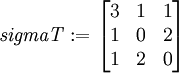
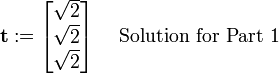
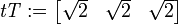
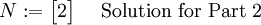
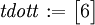
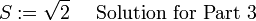

![\mathit{dirPrin} := [1, \,1, \,\{[-1, \,1, \,1]\}], \,[-2, \,1,
\,\{[0, \,-1, \,1]\}], \,[4, \,1, \,\{[2, \,1, \,1]\}]](../I/m/40d3b3328a32d7a2c4431f26f717c5b0.png)
![[1, \,1, \,\{[-1, \,1, \,1]\}]
~~~~ \text{Solution for Part 5}](../I/m/6508767b7016ea4099bb82a724de3504.png)
![[-2, \,1, \,\{[0, \,-1, \,1]\}]
~~~~ \text{Solution for Part 5}](../I/m/dd1c063a89ce5b16562444173249d3d7.png)
![[4, \,1, \,\{[2, \,1, \,1]\}]
~~~~ \text{Solution for Part 5}](../I/m/1089d953d634361603f84bb26ae198f0.png)