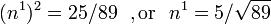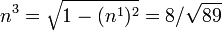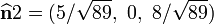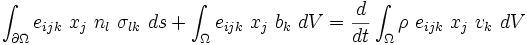Introduction to Elasticity/Sample midterm 4
< Introduction to ElasticitySample Homework Problem 4
Part (a)
A solid is subjected to stresses as shown by the arrows in the figure below. Indicate the indices for each of the stress components, and whether the stresses should be positive or negative.
Solution
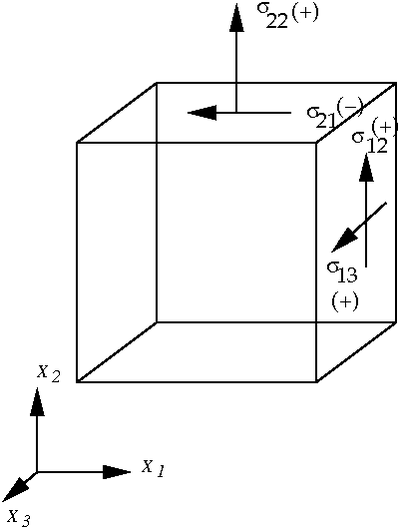 Stress components |
Part (b)
Suppose that the stress tensor field in a body is given by
Find the body force distribution required to maintain equilibrium. (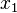 ,
, 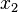 , and
, and 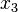 are in meters). Show units.
are in meters). Show units.
Solution
The equation of equilibrium is
Therefore,
or,
The required body forces are (in MN/m )
)
Part (c)
Find the surface tractions at the internal point 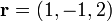 in the body on an internal surface with a surface normal
in the body on an internal surface with a surface normal 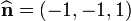 .
.
Solution
The surface traction is given by
The stress at point 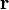 is
is
Therefore,
The traction vector is (after converting 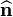 into a unit normal)
into a unit normal)
Part (d)
Find the hydrostatic and deviatoric stress at the point 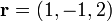 .
.
Solution
The hydrostatic stress is given by
In this case,
Therefore,
The deviatoric stress is given by
Therefore,
Part (e)
Find the principal stresses at this point.
Solution
The principal stresses can be found using the equation
where 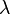 is a principal stress. In expanded form,
is a principal stress. In expanded form,
Substituting the values of stress into the above equation,
Expanding out,
or,
or,
or,
Thus, the first possible value of 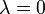 MPa. Also,
MPa. Also,
Therefore,
The principal stresses are (in MPa)
Part (f)
Find the principal direction corresponding to the intermediate principal stress.
Solution
The directions of the principal stresses can be found using the equation
For the principal direction 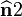 (corresponding to the principal stress
(corresponding to the principal stress 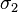 , we have,
, we have,
Hence,
gives us 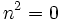 and
and
Now, 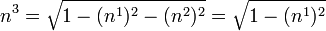 .
Therefore,
.
Therefore,
Taking squares of both sides,
So we get,
Therefore,
The direction corresponding to the intermediate principal stress is
Part (g)
The symmetry of the stress tensor can be derived from a certain balance principle. Name the principle and write it down in index notation.
Solution
The balance principle is
In index notation
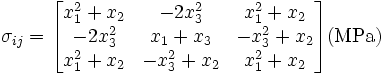
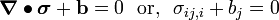
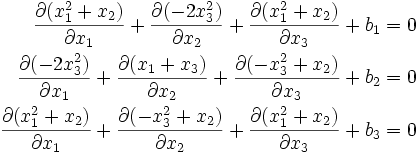
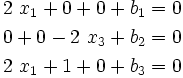
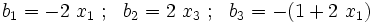
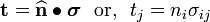
![\left[\boldsymbol{\sigma}\right] = \begin{bmatrix}
0 & -8 & 0 \\ -8 & 3 & -5 \\ 0 & -5 & 0
\end{bmatrix}~(\text{MPa})](../I/m/1f261c8be36afe672d7ec974eae9db42.png)
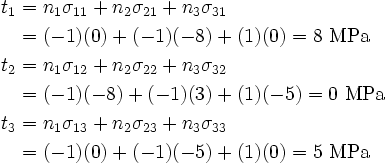
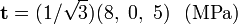
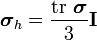
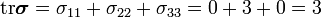
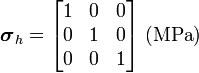
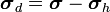
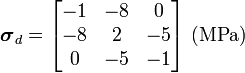
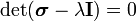
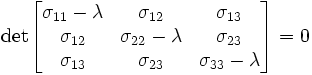
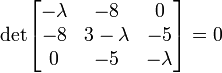
![-\lambda\left[(3-\lambda)(-\lambda) - (-5)(-5)\right] -
(-8)\left[(-8)(-\lambda) - (-5)(0)\right] = 0](../I/m/468086b62b77e78d0cebe608fe361a43.png)
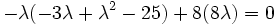
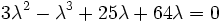
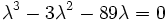
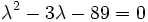
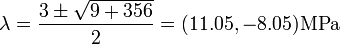
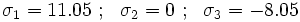
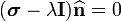
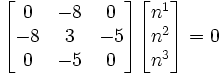
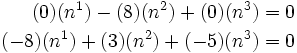
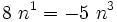
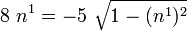
![64(n^1)^2 = 25\left[1-(n^1)^2\right]](../I/m/f8de5a628dafec917f7a44ff6fd4f1f9.png)