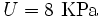Introduction to Elasticity/Sample midterm3

Sample Homework Problem 3

For an isotropic material with 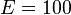$E = 100$ GPa and 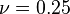$\nu = 0.25$ , find the stress tensor and strain energy density at a point in a body if the components of the strain tensor are given by

\varepsilon_{ij} = \begin{bmatrix} 200 & 100 & 0 \\ 100 & 200 & 100 \\ 0 & 100 & 0 \end{bmatrix} \times 10^{-6}~~.

Solution

The shear modulus (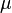 $\mu$ ) is given by

\mu = \frac{E}{2(1+\nu)} = \frac{100}{2.5} = 40~\text{GPa} = 40\times 10^6 ~\text{KPa}

The Lamé modulus (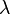 $\lambda$ ) is given by

\lambda = \frac{E\nu}{(1+\nu)(1-2\nu)} = \frac{25}{(1.25)(0.5)} = 40~\text{GPa} = 40\times 10^6 ~\text{KPa}

The stress-strain relation for isotropic materials is

\begin{align} \sigma_{ij} & = 2\mu\varepsilon_{ij} + \lambda\varepsilon_{kk}\delta_{ij} \\ & = 40(2\varepsilon_{ij} + \varepsilon_{kk}\delta_{ij}) \end{align}

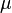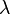Therefore, (after converting $\mu$ and $\lambda$ into KPa so that the 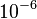$10^{-6}$ term in the strain cancels out),

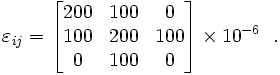
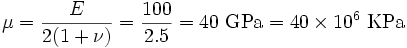
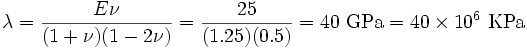
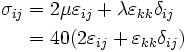
\begin{align} \sigma_{11} & = 40(2\varepsilon_{11} + \varepsilon_{11} + \varepsilon_{22} + \varepsilon_{33}) \\ & = 40\left[(3)(200) + 200 + 0\right] = (40)(800) = 32000 \\ \sigma_{22} & = 40(2\varepsilon_{22} + \varepsilon_{11} + \varepsilon_{22} + \varepsilon_{33}) \\ & = 40\left[(3)(200) + 200 + 0\right] = (40)(800) = 32000 \\ \sigma_{33} & = 40(2\varepsilon_{33} + \varepsilon_{11} + \varepsilon_{22} + \varepsilon_{33}) \\ & = 40\left[(3)(0) + 200 + 200\right] = (40)(400) = 16000 \\ \sigma_{23} & = 40(2\varepsilon_{23}) = (40)(200) = 8000\\ \sigma_{31} & = 40(2\varepsilon_{31}) = (40)(0) = 0\\ \sigma_{12} & = 40(2\varepsilon_{12}) = (40)(200) = 8000 \end{align}

In 3 $\times$ 3 matrix form (after converting into MPa from KPa)

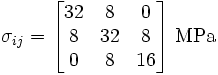
{ \sigma_{ij} = \begin{bmatrix} 32 & 8 & 0 \\ 8 & 32 & 8 \\ 0 & 8 & 16 \end{bmatrix} ~\text{MPa} }

The strain energy density is given by

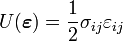
U(\boldsymbol{\varepsilon}) = \frac{1}{2} \sigma_{ij}\varepsilon_{ij}

Therefore,

\begin{align} U(\boldsymbol{\varepsilon}) & = \frac{1}{2}\left[ \sigma_{11} \varepsilon_{11} + \sigma_{22} \varepsilon_{22} + \sigma_{33} \varepsilon_{33} + 2 \sigma_{23} \varepsilon_{23} + 2 \sigma_{31} \varepsilon_{31} + 2 \sigma_{12} \varepsilon_{12} \right] \\ & = \frac{1}{2}\left[(32)(200) + (32)(200) + (16)(0) + (2)(8)(100) + (2)(0)(0) + (2)(8)(100)\right]~\text{Pa}\\ & = \frac{1}{2}\left[6400 + 6400 + 1600 + 1600\right]~\text{Pa}\\ & = 8000~\text{Pa} = 8 ~\text{KPa} \end{align}

The strain energy density is

{ U = 8~\text{KPa}}

This article is issued from Wikiversity - version of the Tuesday, August 07, 2007. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.