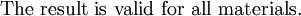Introduction to Elasticity/Sample midterm 2
< Introduction to ElasticitySample Midterm Problem 2
Given:
A strain gage rosette provides the following data
where the 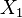 and
and 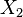 directions are perpendicular to each other and
directions are perpendicular to each other and
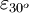 is the extensional strain of a line element at an angle of
is the extensional strain of a line element at an angle of
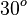 to the
to the 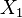 axis (in the counterclockwise direction).
axis (in the counterclockwise direction).
Find:
- (a) Compute
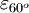 .
. - (b) Is the result valid if the material is anisotropic ?
Solution
Part (a)
From the previous problem, for an angle of rotation of 30 , the rotation matrix
, the rotation matrix ![\left[L\right]](../I/m/4b0b5626c000c7623854a4005aa2b519.png) is
is
Therefore, the components of strain in the rotated co-ordinate system are given by
Since we are given 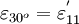 , we will calculate the value of this strain in terms of the original components of strain. Thus,
, we will calculate the value of this strain in terms of the original components of strain. Thus,
Therefore,
Hence,
Next, for an angle of rotation of 60 , the matrix
, the matrix ![\left[L\right]](../I/m/4b0b5626c000c7623854a4005aa2b519.png) is
is
Therefore, 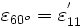 , is given by
, is given by
Therefore,
Part (b)
This article is issued from Wikiversity - version of the Sunday, October 19, 2008. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
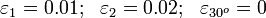
![l_{ij} = \left[L\right] = \begin{bmatrix}
\sqrt{3}/2 & 1/2 & 0 \\
-1/2 & \sqrt{3}/2 & 0 \\
0 & 0 & 1
\end{bmatrix}](../I/m/48cf0e921f9e4e97ae1cf8da1e6ec8fb.png)
![\left[\boldsymbol{\varepsilon}\right]^{'} = \left[L\right] \left[\boldsymbol{\varepsilon}\right] \left[L\right]^T ~~\text{or,}~~
\varepsilon^{'}_{ij} = l_{ip} l_{jq} \varepsilon_{pq}](../I/m/08bdecd45b72d17ea66634b1f2619cf6.png)
![\begin{align}
\varepsilon^{'}_{11} = & l_{1p} l_{1q} \varepsilon_{pq} \\
= & l_{11}l_{11}\varepsilon_{11} + l_{12}l_{11}\varepsilon_{21} + l_{13}l_{11}\varepsilon_{31} +
l_{11}l_{12}\varepsilon_{12} + l_{12}l_{12}\varepsilon_{22} + l_{13}l_{12}\varepsilon_{32} +\\
& l_{11}l_{13}\varepsilon_{13} + l_{12}l_{13}\varepsilon_{23} + l_{13}l_{13}\varepsilon_{33} \\
= & l_{11}(l_{11}\varepsilon_{11} + l_{12}\varepsilon_{12} + l_{13}\varepsilon_{13}) +
l_{12}(l_{11}\varepsilon_{21} + l_{12}\varepsilon_{22} + l_{13}\varepsilon_{23}) + \\
& l_{13}(l_{11}\varepsilon_{31} + l_{12}\varepsilon_{32} + l_{13}\varepsilon_{33}) \\
= & (\frac{\sqrt{3}}{2})\left[(\frac{\sqrt{3}}{2})(0.01) + (\frac{1}{2})\varepsilon_{12}\right] +
(\frac{1}{2})\left[(\frac{\sqrt{3}}{2})\varepsilon_{12} + (\frac{1}{2})(0.02)\right] \\
= & (3/4)(0.01) + (\sqrt{3}/2)\varepsilon_{12} + (1/4)(0.02) \\
= & (5/4)(0.01) + (\sqrt{3}/2)\varepsilon_{12}
\end{align}](../I/m/3f504fce1259908a208e1c450b90cf42.png)
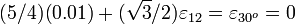
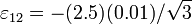
![\begin{align}
\left[L\right] &= \begin{bmatrix}
\cos(60^o) & \sin(60^o) & \cos(90^o) \\
-\sin(60^o) & \cos(60^o) & \cos(90^o) \\
\cos(90^o) & \cos(90^o) & \cos(0^o)
\end{bmatrix} \\
&= \begin{bmatrix}
1/2 & \sqrt{3}/2 & 0 \\
-\sqrt{3}/2 & 1/2 & 0 \\
0 & 0 & 1
\end{bmatrix}
\end{align}](../I/m/6ed5145377f890c68fd88f7555bd72b4.png)
![\begin{align}
\varepsilon^{'}_{11} = & l_{1p} l_{1q} \varepsilon_{pq} \\
= & l_{11}l_{11}\varepsilon_{11} + l_{12}l_{11}\varepsilon_{21} + l_{13}l_{11}\varepsilon_{31} +
l_{11}l_{12}\varepsilon_{12} + l_{12}l_{12}\varepsilon_{22} + l_{13}l_{12}\varepsilon_{32} +\\
& l_{11}l_{13}\varepsilon_{13} + l_{12}l_{13}\varepsilon_{23} + l_{13}l_{13}\varepsilon_{33} \\
= & l_{11}(l_{11}\varepsilon_{11} + l_{12}\varepsilon_{12} + l_{13}\varepsilon_{13}) +
l_{12}(l_{11}\varepsilon_{21} + l_{12}\varepsilon_{22} + l_{13}\varepsilon_{23}) + \\
& l_{13}(l_{11}\varepsilon_{31} + l_{12}\varepsilon_{32} + l_{13}\varepsilon_{33}) \\
= & (\frac{1}{2})\left[(\frac{1}{2})(0.01) + (\frac{\sqrt{3}}{2})\varepsilon_{12}\right] +
(\frac{\sqrt{3}}{2})\left[(\frac{1}{2})\varepsilon_{12} + (\frac{\sqrt{3}}{2})(0.02)\right] \\
= & (1/4)(0.01) + (\sqrt{3}/2)\varepsilon_{12} + (3/4)(0.02) \\
= & (7/4)(0.01) + (\sqrt{3}/2)(-(2.5)(0.01)/\sqrt{3} ) \\
= & (7/4)(0.01) - (5/4)(0.01) = (1/2)(0.01) = 0.005 \\
\end{align}](../I/m/1908a771c18deba9f7742d622e859a3b.png)