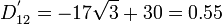Introduction to Elasticity/Sample midterm 1
< Introduction to ElasticitySample Midterm Problem 1
Given:
The vectors 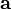 ,
, 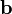 , and
, and 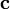 are given, with respect to an orthonormal
basis
are given, with respect to an orthonormal
basis 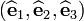 , by
, by
Find:
- (a) Evaluate
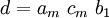 .
. - (b) Evaluate
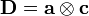 . Is
. Is 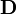 a tensor? If not, why not? If yes, what is the order of the tensor?
a tensor? If not, why not? If yes, what is the order of the tensor? - (c) Name and define
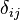 and
and 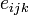 .
. - (d) Evaluate
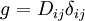 .
. - (e) Show that
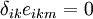 .
. - (f) Rotate the basis
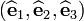 by 30 degrees in the counterclockwise direction around
by 30 degrees in the counterclockwise direction around 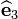 to obtain a new basis
to obtain a new basis 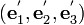 . Find the components of the vector
. Find the components of the vector 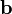 in the new basis
in the new basis 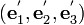 .
. - (g) Find the component
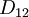 of
of 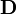 in the new basis
in the new basis 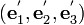 .
.
Solution
Part (a)
Part (b)
Part (c)
Part (d)
Part (e)
Because 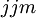 cannot be an even or odd permutation of
cannot be an even or odd permutation of 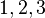 .
.
Part (f)
The basis transformation rule for vectors is
where
Therefore,
Hence,
Thus,
Part (g)
The basis transformation rule for second-order tensors is
Therefore,
This article is issued from Wikiversity - version of the Friday, January 04, 2008. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
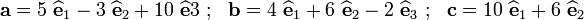
 = 128](../I/m/b33ad9d1429b0c41666d32a1ab19ba83.png)
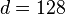
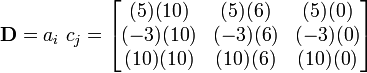
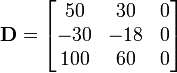
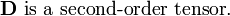
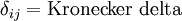
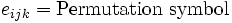
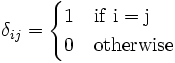
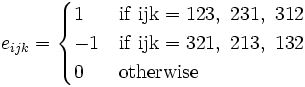
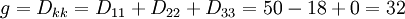
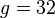
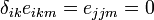
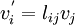
![\begin{align}
\left[L\right] &= \begin{bmatrix}
\cos(30^o) & \cos(90^o-30^o) & \cos(90^o) \\
\cos(90^o+30^o) & \cos(30^o) & \cos(90^o) \\
\cos(90^o) & \cos(90^o) & \cos(0^o)
\end{bmatrix} \\
&= \begin{bmatrix}
\cos(30^o) & \sin(30^o) & \cos(90^o) \\
-\sin(30^o) & \cos(30^o) & \cos(90^o) \\
\cos(90^o) & \cos(90^o) & \cos(0^o)
\end{bmatrix} \\
&= \begin{bmatrix}
\sqrt{3}/2 & 1/2 & 0 \\
-1/2 & \sqrt{3}/2 & 0 \\
0 & 0 & 1
\end{bmatrix}
\end{align}](../I/m/dc7f3a7a6aa3d7be9b52309e2428dfb6.png)
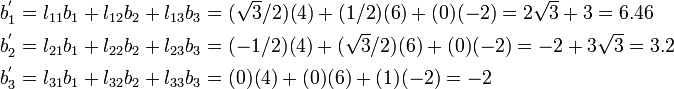

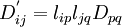
![\begin{align}
D_{12}^{'} = &
l_{11} l_{21} D_{11} + l_{12} l_{21} D_{21} + l_{13} l_{21} D_{31} +
l_{11} l_{22} D_{12} + l_{12} l_{22} D_{22} + l_{13} l_{22} D_{32} +\\
& l_{11} l_{23} D_{13} + l_{12} l_{23} D_{23} + l_{13} l_{23} D_{33} \\
= & l_{11} (l_{21} D_{11} + l_{22} D_{12} + l_{23} D_{13}) +
l_{12} (l_{21} D_{21} + l_{22} D_{22} + l_{23} D_{23}) +\\
& l_{13} (l_{21} D_{31} + l_{22} D_{32} + l_{23} D_{33}) \\
= & (\frac{\sqrt{3}}{2})\left[(-\frac{1}{2})(50)+(\frac{\sqrt{3}}{2})(30)+(0)(0)\right] +
(\frac{1}{2})\left[(-\frac{1}{2})(-30)+(\frac{\sqrt{3}}{2})(-18)+(0)(0)\right] + \\
& (0)\left[(-\frac{1}{2})(100)+(\frac{\sqrt{3}}{2})(60)+(0)(0)\right]\\
= & (\frac{\sqrt{3}}{2})\left[-25+ 15\sqrt{3}\right] +
(\frac{1}{2})\left[15 - 9\sqrt{3}\right] \\
= & -25\frac{\sqrt{3}}{2} + \frac{45}{2} + \frac{15}{2} - 9\frac{\sqrt{3}}{2} \\
= & -17\sqrt{3} + 30
\end{align}](../I/m/6e7f8df3ea325fe690edd7def42ccc05.png)