Introduction to Elasticity/Sample final 2
< Introduction to ElasticitySample Final Exam Problem 2
A long elastic cylinder with flat end caps is constructed from 7075 T6 Aluminum alloy. The cylinder has an outer radius of 10 cm and a thickness of 5 mm. The material has a Young's modulus of 72 GPa, a Poisson's ratio of 0.33 and a yield stress under uniaxial tension of 500 MPa. A circular hole of diameter 10 mm is drilled through the thickness of the cylinder so that the contents of the inside can be viewed. The ends of the drilled hole are covered with a strong, flexible and transparent membrane to allow for visibility.
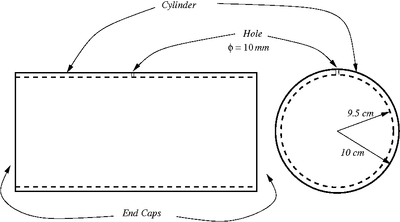 Aluminum cylinder with end caps |
The inside of the cylinder is now pressurized uniformly to a pressure of 20 MPa.
- (a) Give estimates of the magnitudes of the maximum and minimum hoop stress at the drilled hole (using a coordinate system that is centered on the hole).
- (b) Does the stress state at the hole lead to the yielding of the Aluminum alloy? Use the von Mises yield criterion
Clearly state all the non-standard assumptions that you make.
Solution
The stress field in a cylinder with end caps under internal pressure can be approximated (using plane-strain) by
At the inner radius of the cylinder  . Therefore,
. Therefore,
At the outer radius of the cylinder 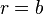 . Therefore,
. Therefore,
At this stage, we make a few assumptions
- Because the cylinder is thin, we can assume that the stresses at
 represent the state of stress in the cylinder.
represent the state of stress in the cylinder. - Because the radius of the cylinder is large compared to the radius of the drilled hole, we can consider the cylinder to be approximated by an infinite plate.
- Because the diameter of the drilled hole is larger than the thickness of the cylinder, we can assume plane stress conditions.
- We neglect the radial stress in the cylinder because it is small compared to the hoop and axial stresses.
The problem is then converted into one of a circular hole in an infinite thin plate under biaxial tension with 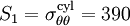 MPa and
MPa and 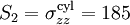 MPa.\\
MPa.\\
For a plate with a circular under uniaxial tension (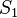 ), the stresses are
), the stresses are
At the drilled hole  . Therefore,
. Therefore,
To get the solution for a biaxial stress field, we superpose the solution in a coordinate system where 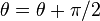 , which is,
, which is,
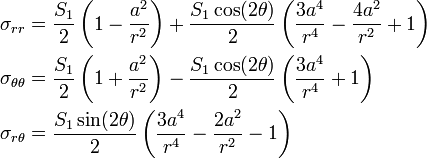
Therefore, the stress field at the drilled hole is
The stress 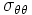 at the hole is a maximum or minimum when
at the hole is a maximum or minimum when 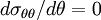 , i.e.,
, i.e.,
The hoop stresses at the drilled hole for these values of 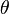 are
are
The maximum and minimum hoop stresses at the hole are 985 MPa and 165 MPa, respectively.
At the hole, the maximum principal stress is 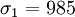 MPa. The
remaining principal stresses are
MPa. The
remaining principal stresses are 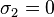 ,
, 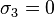 . Therefore,
the von Mises yield stress is given by
. Therefore,
the von Mises yield stress is given by
The uniaxial yield strength of the cylinder is 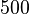 MPa, which is considerably lower than the von Mises yield stress.
MPa, which is considerably lower than the von Mises yield stress.
The material around the hole will yield under the applied pressure.
![\sigma^2_{Y} = \frac{1}{2}\left[(\sigma_1 - \sigma_2)^2 +
(\sigma_2 - \sigma_3)^2+ (\sigma_3 - \sigma_1)^2\right]~.](../I/m/a5063cd3acad38c3312ed077ca5ffedf.png)
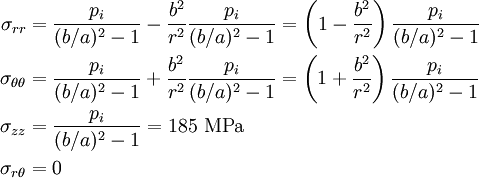
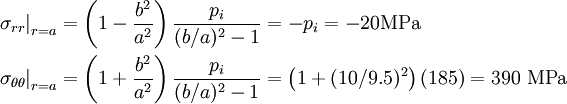
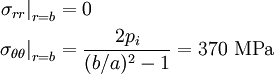
![\begin{align}
\sigma_{rr} & = 0 \\
\sigma_{\theta\theta} & = S_1[1 - 2\cos(2\theta)]\\
\sigma_{r\theta} & = 0
\end{align}](../I/m/e7d1a22f90a3f74b27436b2ecdc049e6.png)
![\begin{align}
\sigma_{rr} & = 0 \\
\sigma_{\theta\theta} & = S_2[1 + 2\cos(2\theta)]\\
\sigma_{r\theta} & = 0
\end{align}](../I/m/622948a083b5751fdda301a715544633.png)
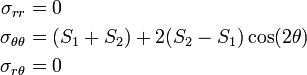
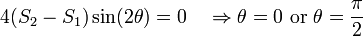
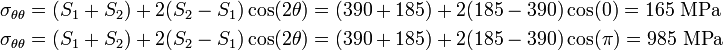
![\sigma_{Y} = \sqrt{\frac{1}{2}\left[(\sigma_1 - \sigma_2)^2 +
(\sigma_2 - \sigma_3)^2+ (\sigma_3 - \sigma_1)^2\right]}
= \sigma_1](../I/m/fae6cf621122ee751aa9ec22e7fd78d4.png)