Introduction to Elasticity/Rotating rectangular beam
< Introduction to ElasticityExample : Rotating Rectangular Beam
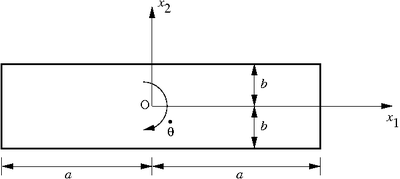 A rotating rectangular beam |
The body force potential is given by
Hence,
or,
The compatibility condition (in terms of stress) is
Plug 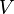 in to get
in to get
Since 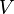 is even in
is even in 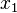 and
and 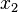 and BCs are homogeneous, assume
and BCs are homogeneous, assume
Hence,
The traction BCs are
Apply BCs at 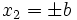 .
.
Therefore,
We then have,
Plug into compatibility equation
to get
or,
Apply BCs at 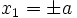 .
.
Strong BCs imply that
which cannot be true. So weak BCs on 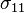 need to be applied at
need to be applied at 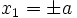 .
.
Hence,
or,
Hence,
The stress field is, therefore,
or,
The displacements can be found in the standard manner.
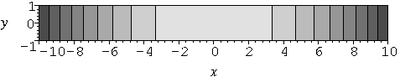 Stresses ( 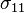 ) in a rotating rectangular beam ) in a rotating rectangular beam |
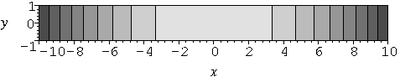 Stresses ( 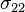 ) in a rotating rectangular beam ) in a rotating rectangular beam |
This article is issued from Wikiversity - version of the Saturday, January 30, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
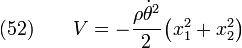
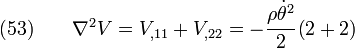
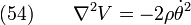
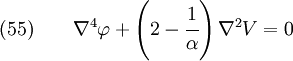
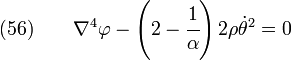
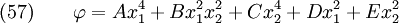
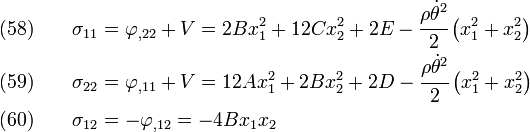
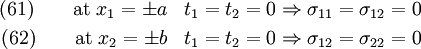
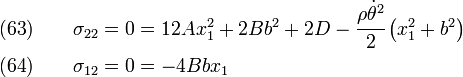
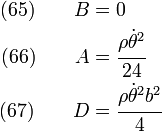
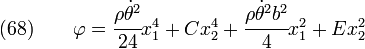
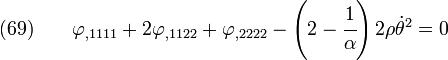
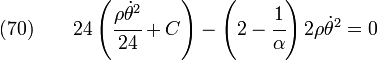
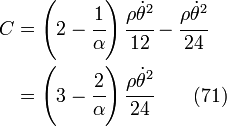
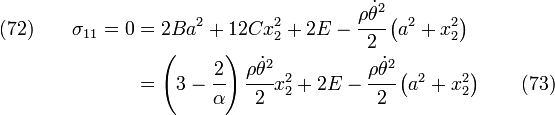
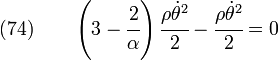
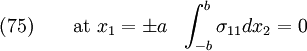
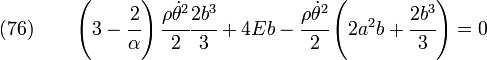
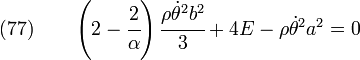
![\text{(78)} \qquad
E = \cfrac{\rho\dot{\theta}^2}{4}\left[a^2-
\left(2-\cfrac{2}{\alpha}\right)\cfrac{b^2}{3} \right]](../I/m/0691fd5136be4ce3ceb6d0900ac45a90.png)
![\begin{align}
\text{(79}) \qquad \sigma_{11} & =
\left(3-\cfrac{2}{\alpha}\right) \cfrac{\rho\dot{\theta}^2}{2} x_2^2 +
\cfrac{\rho\dot{\theta}^2}{2}\left[a^2-
\left(2-\cfrac{2}{\alpha}\right)\cfrac{b^2}{3} \right]
-\cfrac{\rho\dot{\theta}^2}{2} \left(x_1^2 + x_2^2\right)\\
\text{(80}) \qquad \sigma_{22} & =
\cfrac{\rho\dot{\theta}^2}{2} x_1^2 +
\cfrac{\rho\dot{\theta}^2b^2}{2}
-\cfrac{\rho\dot{\theta}^2}{2} \left(x_1^2 + x_2^2\right) \\
\qquad \sigma_{12} & = 0
\end{align}](../I/m/d11ada8b7f33e016caa0004ebbdd09b8.png)
![\begin{align}
\text{(81)} \qquad \sigma_{11} & = \cfrac{\rho\dot{\theta}^2}{2}\left[\left(a^2 - x_1^2\right)+
2\left(1-\cfrac{1}{\alpha}\right)\left(x_2^2-\cfrac{b^2}{3}\right)\right]
\\
\text{(82)} \qquad \sigma_{22} & = \cfrac{\rho\dot{\theta}^2}{2}\left(b^2 - x_2^2\right)
\\
\sigma_{12} & = 0
\end{align}](../I/m/80d9fc4211817046bd759d0ffb60927b.png)