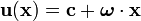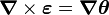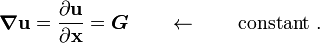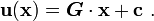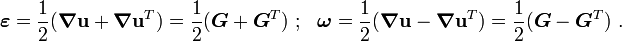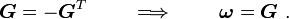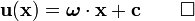Introduction to Elasticity/Rigid body motions
< Introduction to ElasticityRigid body motions
Rigid Deformation
A rigid deformation has the form
where  are fixed material points and
are fixed material points and 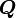 is an orthogonal (rotation) tensor.
is an orthogonal (rotation) tensor.
Therefore
and
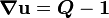 .
.
The strain tensors in this case are given by
but
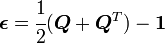 .
.
Hence the infinitesimal strain tensor does not measure the correct strain when there are large rotations though the finite strain tensor can.
Rigid Displacement
Rigid displacements involve motions in which there are no strains.
|
Properties of rigid displacement fields If |
Finite Rigid Displacement
If the displacement is rigid we have
Infinitesimal Rigid Displacement
An infinitesimal rigid displacement is given by
where 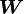 is a skew tensor.
is a skew tensor.
Rigid body displacement field
Show that, for a rigid body motion with infinitesimal rotations, the
displacement field 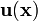 for can be expressed as
for can be expressed as
where 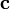 is a constant vector and
is a constant vector and 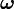 is the infinitesimal
rotation tensor.
is the infinitesimal
rotation tensor.
Proof:
Note that for a rigid body motion, the strain 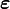 is zero. Since
is zero. Since
we have a 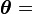 constant when
constant when 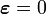 , i.e., the rotation is
homogeneous.
, i.e., the rotation is
homogeneous.
For a homogeneous deformation, the displacement gradient is
independent of 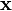 , i.e.,
, i.e.,
Integrating, we get
Now the strain and rotation tensors are given by
For a rigid body motion, the strain 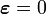 . Therefore,
. Therefore,
Plugging into the expression for 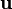 for a homogeneous deformation, we
have
for a homogeneous deformation, we
have
![\boldsymbol{\varphi}(\mathbf{X}) = \mathbf{X}_1 + \boldsymbol{Q}\bullet[\mathbf{X}-\mathbf{X}_0]](../I/m/8be89ebbbe919e943af78d2734fee1a7.png)
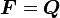
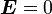
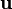 is a rigid displacement field, then the strain field corresponding to
is a rigid displacement field, then the strain field corresponding to ![\begin{align}
\mathbf{u}(\mathbf{X}) &= \mathbf{X}_1 + \boldsymbol{\nabla}\mathbf{u}\bullet[\mathbf{X}-\mathbf{X}_0] + \boldsymbol{1}[\mathbf{X}-\mathbf{X}_0] - \mathbf{X} \\
& = (\mathbf{X}_1-\mathbf{X}_0) + \boldsymbol{\nabla}\mathbf{u}\bullet[\mathbf{X}-\mathbf{X}_0] \\
&= \mathbf{u}_0 + \boldsymbol{\nabla}\mathbf{u}\bullet[\mathbf{X}-\mathbf{X}_0] \end{align}](../I/m/c60c7d38d68fc34435949dfe8180efde.png)
![\mathbf{u}(\mathbf{X}) = \mathbf{u}_0 + \boldsymbol{W}\bullet[\mathbf{X}-\mathbf{X}_0]](../I/m/37e5d41f2da8d2bf2d60d979b0c3a17e.png)