Introduction to Elasticity/Principle of minimum potential energy
< Introduction to ElasticityStrain Energy Density
The strain energy density is defined as
If the strain energy density is path independent, then it acts as a potential for stress, i.e.,
For adiabatic processes, 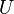 is equal to the change in internal energy per unit volume.
is equal to the change in internal energy per unit volume.
For isothermal processes, 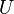 is equal to the Helmholtz free energy per unit volume.
is equal to the Helmholtz free energy per unit volume.
The natural state of a body is defined as the state in which the body is in stable thermal equilibrium with no external loads and zero stress and strain.
When we apply energy methods in linear elasticity, we implicitly assume that a body returns to its natural state after loads are removed. This implies that the Gibb's condition is satisfied :
Principle of Minimum Potential Energy
This principle states that
- If the prescribed traction and body force fields are independent of the deformation
- then the actual displacement field makes the potential energy functional an absolute minimum.
In other words, the principle of minimum potential energy states that the potential energy functional
is minimized by the actual displacement field.
Proof
The first step in the proof is to show that the actual displacements make the function 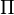 stationary. The second step is to show that the stationary point is actually the minimum.
stationary. The second step is to show that the stationary point is actually the minimum.
Proof of the Principle of Stationary Potential Energy
The first variation of the potential energy functional 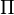 is
is
or,
or,
Therefore, ![\delta\Pi[\mathbf{u},\delta\mathbf{u}] = 0](../I/m/7aa664514ea7f8c1e850485f313f22d9.png) (i.e.
(i.e. 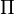 is stationary) only if
is stationary) only if
which are the conditions that only the actual displacement field satisfies.
Proof of the Principle of Minimum Potential Energy
To prove that ![\Pi[\mathbf{u},\delta\mathbf{u}]](../I/m/004f8c0abde5c810d10735c4e0830a91.png) is not only stationary, but also
the global minimum all we now need to show is that
is not only stationary, but also
the global minimum all we now need to show is that
Now,
If the displacement field is a pure rigid body motion, then the strain energy density
where 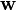 is the spin tensor given by
is the spin tensor given by
If the displacement field does not contain any rigid body motion, then the strain energy density is given by
where 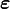 is the strain tensor given by
is the strain tensor given by
Therefore, for a displacement field containing both spin and strain
or,
This means that 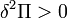 for all values of
for all values of 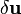 other
than rigid body motion, in which case
other
than rigid body motion, in which case 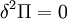 .
.
Hence, for mixed boundary value problems 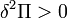 for all
for all
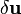 , as long as the displacement BCs prevent rigid body motions.
Therefore, the potential energy functional is minimized by the actual
displacement field.
, as long as the displacement BCs prevent rigid body motions.
Therefore, the potential energy functional is minimized by the actual
displacement field.
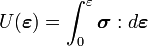
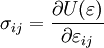
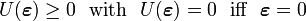
![\Pi[\mathbf{u}] = \frac{1}{2}\int_{\mathcal{B}} \boldsymbol{\sigma}:\boldsymbol{\varepsilon}~dV -
\int_{\mathcal{B}} \mathbf{f}\bullet\mathbf{u}~dV
- \int_{\partial{\mathcal{B}}^t} \mathbf{t}\bullet\mathbf{u}~dA](../I/m/e19083fb0bc2f27b5a8128f83bef8c5f.png)
![\delta\Pi[\mathbf{u},\delta\mathbf{u}] =
\int_B C_{ijkl}~u_{i,j}~\delta u_{k,l}~dV
- \int_B \tilde{f}_i~\delta u_i~dV
- \int_{\partial B^t} \tilde{t}_i~\delta u_i~dA](../I/m/4382e41aeb9b81c99e9455cf0e189db8.png)
![\begin{align}
\delta\Pi[\mathbf{u},\delta\mathbf{u}] & =
\int_B \sigma_{ji}~\delta u_{i,j}~dV
- \int_B \tilde{f}_i~\delta u_i~dV
- \int_{\partial B^t} \tilde{t}_i~\delta u_i~dA \\
& =
\int_B (\sigma_{ji}~\delta u_i)_{,j}~dV
- \int_B \sigma_{ji,j}~\delta u_i~dV
- \int_B \tilde{f}_i~\delta u_i~dV
- \int_{\partial B^t} \tilde{t}_i~\delta u_i~dA \\
& =
\int_{\partial B} \sigma_{ji}~\delta u_i~n_j~dA
- \int_B \sigma_{ji,j}~\delta u_i~dV
- \int_B \tilde{f}_i~\delta u_i~dV
- \int_{\partial B^t} \tilde{t}_i~\delta u_i~dA \\
& =
\int_{\partial B^t} \sigma_{ji}~n_j~\delta u_i~dA
- \int_{\partial B^t} \tilde{t}_i~\delta u_i~dA
- \int_B \sigma_{ji,j}~\delta u_i~dV
- \int_B \tilde{f}_i~\delta u_i~dV \\
& =
\int_{\partial B^t} \left[\sigma_{ji}~n_j-\tilde{t}_i\right]~\delta u_i~dA
- \int_B \left[\sigma_{ji,j} + \tilde{f}_i\right]~\delta u_i~dV
\end{align}](../I/m/3b24a2609b81ffda6b895ede40cc8020.png)
![\delta\Pi[\mathbf{u},\delta\mathbf{u}]=
\int_{\partial B^t} \left[\widehat{\mathbf{n}}{}\bullet\boldsymbol{\sigma}
-\tilde{\mathbf{t}}\right]\bullet\delta\mathbf{u}~dA
- \int_B \left[\boldsymbol{\nabla}\bullet{\boldsymbol{\sigma}} + \tilde{\mathbf{f}}\right]\bullet\delta\mathbf{u}~dV](../I/m/2bd120728f7ed23c382d91248e0f94e7.png)
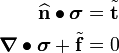
![\delta^2\Pi[\mathbf{u},\delta\mathbf{u}] > 0](../I/m/5911fe84ae051406d6deb2c9435bc6c6.png)
![\delta^2\Pi[\mathbf{u},\delta\mathbf{u}]=
\int_B C_{ijkl}~\delta u_{i,j}~\delta u_{k,l}~dV](../I/m/c167c8b8f899265291a6e9eaa40c2a26.png)
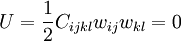
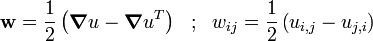
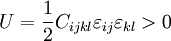
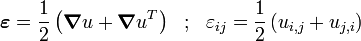
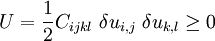
![\delta^2\Pi[\mathbf{u},\delta\mathbf{u}]=
\int_B C_{ijkl}~\delta u_{i,j}~\delta u_{k,l}~dV \ge 0](../I/m/4e0b7089f14a417c2de4a65e2610dca3.png)