Introduction to Elasticity/Principle of minimum complementary energy
< Introduction to ElasticityComplementary Strain Energy
The complementary strain energy density is given by
For linear elastic materials
Principle of Minimum Complementary Energy
Let 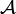 be the set of all statically admissible states of stress.
be the set of all statically admissible states of stress.
Let the complementary energy functional be
Then the Principle of Stationary Complementary Energy states that:
Among all stress fields 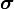 in
in 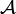 , the functional
, the functional 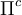 is rendered stationary only by actual stress fields which satisfy compatibility and the displacement BCs.
is rendered stationary only by actual stress fields which satisfy compatibility and the displacement BCs.
The Principle of Minimum Complementary Energy states that:
For linear elastic materials, the complementary energy functional is rendered an absolute minimum by the actual stress field.
Note that the complementary energy corresponding to the actual stress field is the negative of the potential energy corresponding to the actual displacement field.
Proof
Let ![[\mathbf{u},\boldsymbol{\varepsilon},\boldsymbol{\sigma}]](../I/m/6940cd97470d7e2442f959105e4577e5.png) be a solution of a the mixed boundary value problem of linear elasticity.
be a solution of a the mixed boundary value problem of linear elasticity.
Let 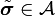 .
.
Define
Then 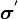 satisfies equilibrium and the traction BCs, i.e.,
satisfies equilibrium and the traction BCs, i.e.,
Since
and
we have,
We can also show that
Therefore,
Now,
Hence,
Therefore,
From equations (1), (2), and (3), we have,
Since 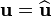 on
on 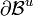 , we have,
, we have,
Hence, proved.
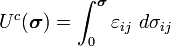
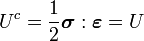
![\Pi^c[\boldsymbol{\sigma}] = \int_{\mathcal{B}} U^c(\boldsymbol{\sigma})~dV - \int_{\partial{\mathcal{B}}^u}
\mathbf{t}\bullet\widehat{\mathbf{u}}~dA](../I/m/9c35915331a6a297e5e69938229eaded.png)
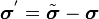
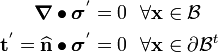
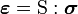
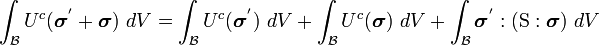
![\text{(1)} \qquad
\int_{\mathcal{B}} \left[U^c(\tilde{\boldsymbol{\sigma}}) - U^c(\boldsymbol{\sigma})\right]~dV =
\int_{\mathcal{B}} U^c(\boldsymbol{\sigma}^{'})~dV +
\int_{\mathcal{B}} \boldsymbol{\sigma}^{'}:\boldsymbol{\varepsilon}~ dV](../I/m/e3fdb4177862c052bf62d390ffd20bb9.png)
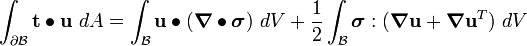
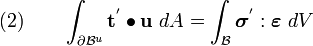
![\Pi^c[\tilde{\boldsymbol{\sigma}}] = \int_{\mathcal{B}} U^c(\tilde{\boldsymbol{\sigma}})~dV -
\int_{\partial{\mathcal{B}}^u} \mathbf{t}\bullet\widehat{\mathbf{u}}~dA](../I/m/a24c9bc8ec96d02d0ff677e880fe1a19.png)
![\text{(3)} \qquad
\Pi^c[\tilde{\boldsymbol{\sigma}}] - \Pi^c[\boldsymbol{\sigma}] =
\int_{\mathcal{B}} \left[U^c(\tilde{\boldsymbol{\sigma}})-U^c(\boldsymbol{\sigma})\right]~dV
- \int_{\partial{\mathcal{B}}^u} \mathbf{t}^{'}\bullet\widehat{\mathbf{u}}~dA](../I/m/ed6a5c91a5a5c7f76624c92c6bcee9ca.png)
![\Pi^c[\tilde{\boldsymbol{\sigma}}] - \Pi^c[\boldsymbol{\sigma}] =
\int_{\mathcal{B}} U^c(\boldsymbol{\sigma}^{'})~dV +
\int_{\partial{\mathcal{B}}^{u}} \mathbf{t}^{'}\bullet\mathbf{u}~dA
- \int_{\partial{\mathcal{B}}^u} \mathbf{t}^{'}\bullet\widehat{\mathbf{u}}~dA](../I/m/8fce920fdc25aa602219180ff8c1914b.png)
![\Pi^c[\tilde{\boldsymbol{\sigma}}] - \Pi^c[\boldsymbol{\sigma}] =
\int_{\mathcal{B}} U^c(\boldsymbol{\sigma}^{'})~dV > 0](../I/m/a422c783806725c1a82f1351b6dc3ab1.png)