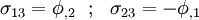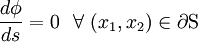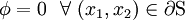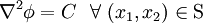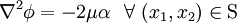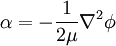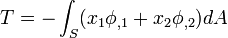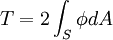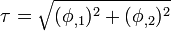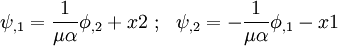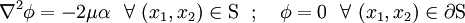Introduction to Elasticity/Prandtl stress function

Prandtl Stress Function ( $\phi$ )

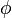The traction free BC is obviously difficult to satisfy if the cross-section is not a circle or an ellipse.

To simplify matters, we define the Prandtl stress function 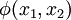$\phi(x_1,x_2)\,$ using

{ \sigma_{13} = \phi_{,2} ~~;~~ \sigma_{23} = -\phi_{,1} }

You can easily check that this definition satisfies equilibrium.

It can easily be shown that the traction-free BCs are satisfied if

{ \frac{d\phi}{ds} = 0 ~~\forall~(x_1,x_2) \in \partial\text{S} }

where $s$ is a coordinate system that is tangent to the boundary.

If the cross section is simply connected, then the BCs are even simpler:

{ \phi = 0 ~~\forall~(x_1,x_2) \in \partial\text{S} }

From the compatibility condition, we get a restrictionon 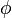$\phi$

{ \nabla^2{\phi} = C ~~\forall~(x_1,x_2) \in \text{S} }

where 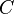$C$ is a constant.

Using relations for stress in terms of the warping function 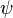$\psi$ , we get

{ \nabla^2{\phi} = -2\mu\alpha ~~\forall~(x_1,x_2) \in \text{S} }

Therefore, the twist per unit length is

{ \alpha = -\frac{1}{2\mu} \nabla^2{\phi} }

The applied torque is given by

{ T = -\int_{S} (x_1 \phi_{,1} + x_2 \phi_{,2}) dA \, }

For a simply connected cylinder,

{ T =2 \int_{S} \phi dA \, }

The projected shear traction is given by

{\tau = \sqrt{(\phi_{,1})^2+ (\phi_{,2})^2}}

The projected shear traction at any point on the cross-section is tangent to the contour of constant 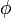$\phi\,$ at that point.

The relation between the warping function 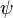$\psi\,$ and the Prandtl stress function 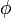$\phi\,$ is

{ \psi_{,1} = \frac{1}{\mu\alpha} \phi_{,2} + x2 ~;~~ \psi_{,2} = -\frac{1}{\mu\alpha} \phi_{,1} - x1 }

Membrane Analogy

The equations

\nabla^2{\phi} = -2\mu\alpha ~~\forall~(x_1,x_2) \in \text{S}~~;~~~ \phi = 0 ~~\forall~(x_1,x_2) \in \partial\text{S}

are similar to the equations that govern the displacement of a membrane that is stretched between the boundaries of the cross-sectional curve and loaded by an uniform normal pressure.

This analogy can be useful in estimating the location of the maximum shear stress and the torsional rigidity of a bar.

The stress function is proportional to the displacement of the membrane from the plane of the cross-section.
The stiffest cross-sections are those that allow the maximum volume to be developed between the deformed membrane and the plane of the cross-section for a given pressure.
The shear stress is proportional to the slope of the membrane.

This article is issued from Wikiversity - version of the Monday, February 01, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Introduction to Elasticity/Prandtl stress function

Prandtl Stress Function ()

Membrane Analogy

Prandtl Stress Function ( $\phi$ )