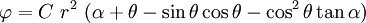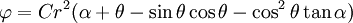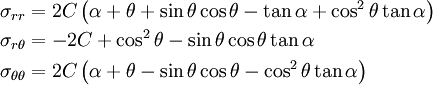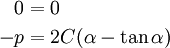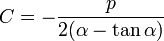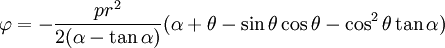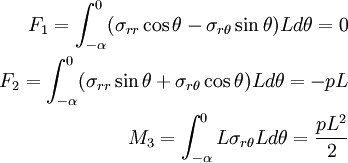Introduction to Elasticity/Polar coordinates
< Introduction to ElasticityThe Edge Dislocation Problem
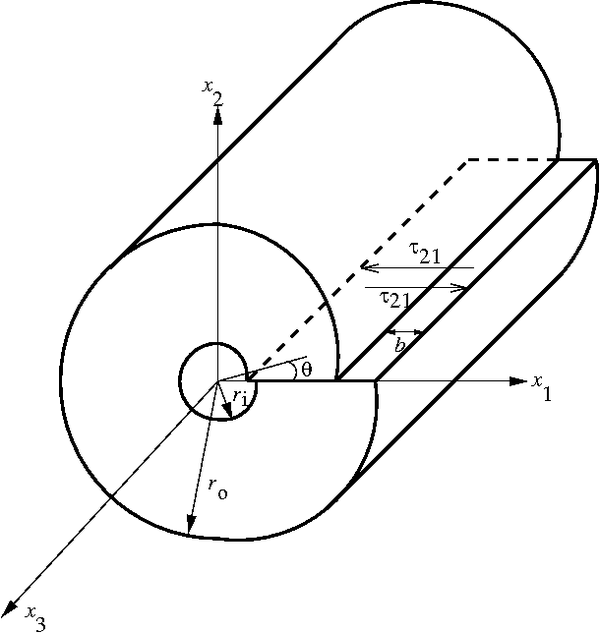 Stress due to an edge dislocation |
Assume that stresses vanish at 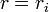 and that
and that 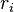 is the radius of an undeformed cylindrical hole. Also stresses vanish at
is the radius of an undeformed cylindrical hole. Also stresses vanish at
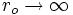 . Relative displacement
. Relative displacement 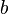 is prescribed on each face of the cut.
is prescribed on each face of the cut.
The edge dislocation problem is a plane strain problem. However, it is not axisymmetric.
It is probable that 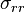 and
and 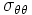 are
symmetric about the
are
symmetric about the 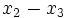 plane. Similarly, it is probable that
plane. Similarly, it is probable that 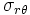 is symmetric about the
is symmetric about the 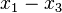 plane.
plane.
These probable symmetries suggest that we can use a stress function of the form
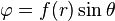
In cylindrical co-ordinates, the gudir beta Airy stress function leads to
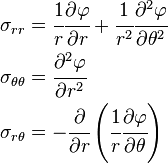
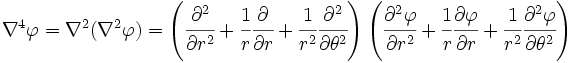
and
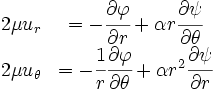
Proceeding as usual, after plugging the value of 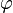 in to
the biharmonic equation, we get
in to
the biharmonic equation, we get
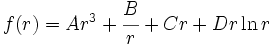
Applying the stress boundary conditions and neglecting terms containing
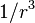 , we get
, we get
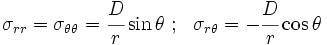
Next we compute the displacements, in a manner similar to that shown
for the cantilever beam problem. The displacement BCs are 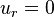 at
at
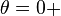 and
and 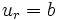 at
at 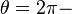 . We can use these
to determine
. We can use these
to determine 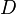 and hence the stresses.
and hence the stresses.
Rigid body motions are eliminated next by enforcing zero displacements
and rotations at 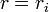 and
and 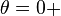 . The final expressions for the displacements can then be obtained.
. The final expressions for the displacements can then be obtained.
Sample homework problems
Problem 1
Consider the Airy stress function
- Show that this stress function provides an approximate solution for a cantilevered triangular beam with a uniform traction
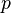 applied to the upper surface. The angle
applied to the upper surface. The angle 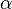 is the angle subtended by the free edges of the triangle.
is the angle subtended by the free edges of the triangle.
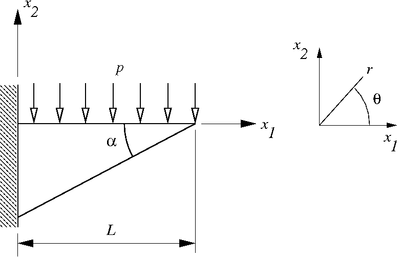 A cantilevered triangular beam with uniform normal traction |
- Find the value of the constant
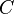 in terms of
in terms of 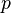 and
and 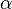 .
.
Solution:
Given:
Using a cylindrical co-ordinate system, the stresses are
At 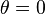 ,
, 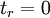 ,
, 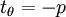 ,
, 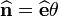 .
Therefore,
.
Therefore, 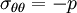 and
and 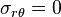 .
.
Hence, the shear traction BC is satisfied and the normal traction BC is satisfied if
At 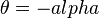 ,
, 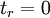 ,
, 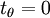 ,
, 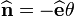 .
Therefore,
.
Therefore, 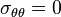 and
and 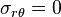 . Both
these BCs are identically satisfied by the stresses (after substituting for
. Both
these BCs are identically satisfied by the stresses (after substituting for 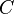 ).
Hence, equilibrium is satisfied.
).
Hence, equilibrium is satisfied.
To satisfy compatibility, 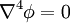 . Use Maple to verify that this is indeed true.
. Use Maple to verify that this is indeed true.
The remaining BC is the fixed displacement BC at the wall. We replace this BC with weak BCs at 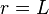 . The traction distribution on the surface
. The traction distribution on the surface
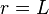 are
are 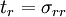 and
and 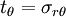 .
The statically equivalent forces and moments are
.
The statically equivalent forces and moments are
You can verify these using Maple.
Hence, the given stress function provides an approximate solution for the cantilevered beam (in the St. Venant sense).